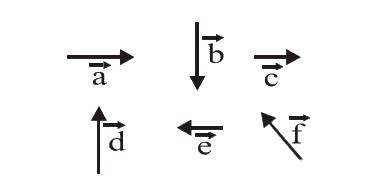A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Six vectors, vec(a) through vec(f) have the magnitudes and directions ...
Text Solution
|
- Two vectors vec a&vec b have equal magnitudes of 10m, Find the magnitu...
Text Solution
|
- The magnitude of vectors vec(OA), vec(OB) and vec (OC) in figure are e...
Text Solution
|
- Six vector vec(a) through vec(f) have the magnitudes and direction ind...
Text Solution
|
- सदिश vec(A) का परिमाण A है vec(A) की दिशा से theta कोण पर A के घटक का...
Text Solution
|
- vec(A) is a vector with magnitude A, then the unit vector hat(A) in th...
Text Solution
|
- विस्थापन सदिश vecS का परिमाण 5 मीटर है तथा दिशा उत्तर की ओर है । निम्...
Text Solution
|
- vec(a)तकvec(f) के छः सदिशों के परिमाण तथा दिशा चित्र में प्रदर्शित है ...
Text Solution
|
- Six vectors hata to hati have the magnitude and directions indicated i...
Text Solution
|