A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
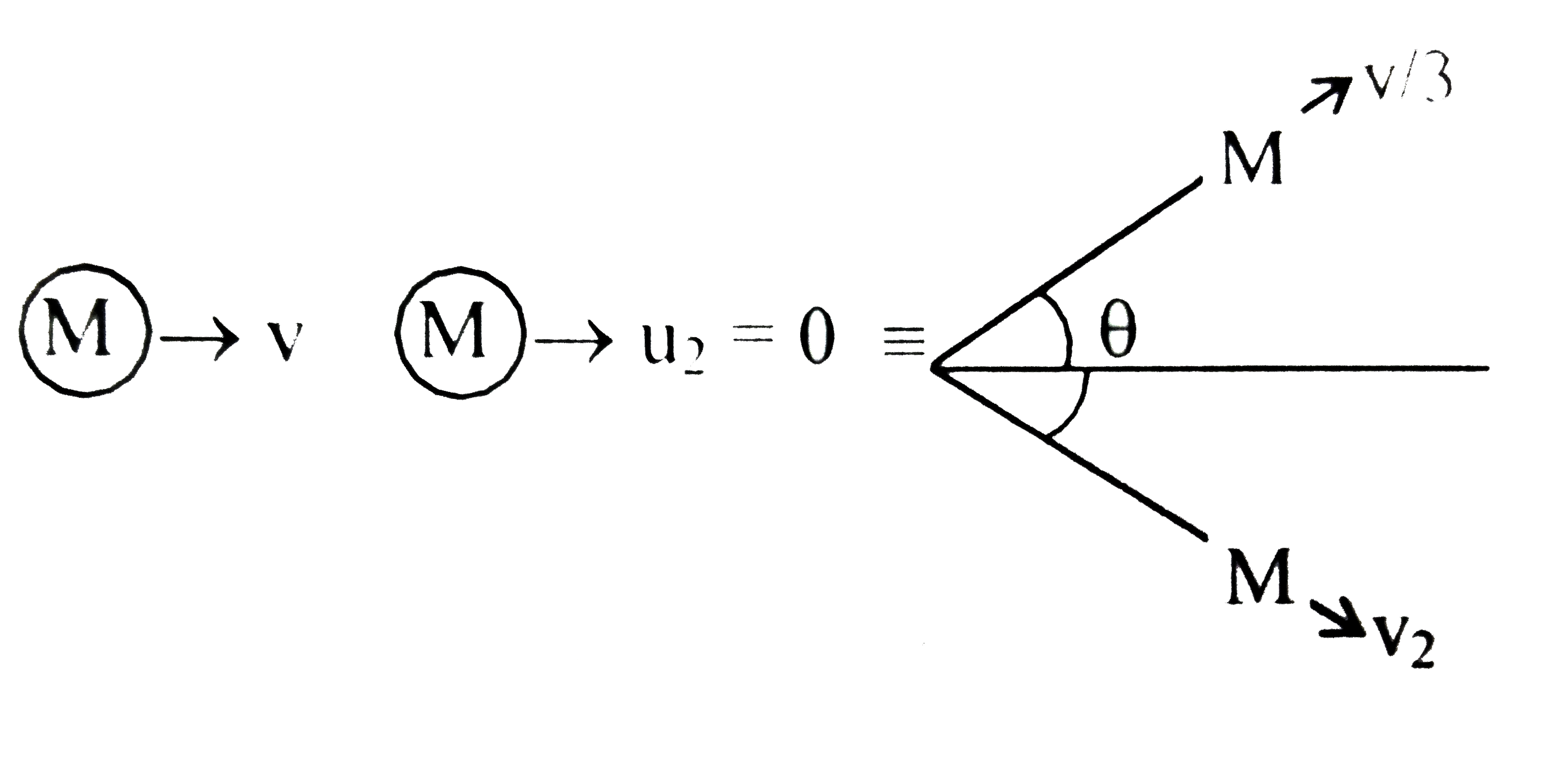
- On a frictionless surface, a block of mass M moving at speed v collide...
Text Solution
|
- On a friction surface a block a mass M moving at speed v collides elas...
Text Solution
|
- किसी घर्षणहीन पृष्ठ पर v चाल से चलता हुआ m द्रव्यमान का एक ब्लॉक, उसी ...
Text Solution
|
- A block of mass 'm' moving on a frictionless surface at speed 'v' coll...
Text Solution
|
- A block of mass M=4kg is moving with velocity V=6m/s toward a target b...
Text Solution
|
- चाल 5 मी/से से गतिमान द्रव्यमान 10 किग्रा का एक गुटका विरामावस्था में ...
Text Solution
|
- On a frictionless surface, a block of mass M moving at a v speed colli...
Text Solution
|
- A block of mass m moving with speed v collides with another block of ...
Text Solution
|
- A block of mass m moving with speed v collides with another block of m...
Text Solution
|