Home
Class 12
PHYSICS
in the given figure, alpha=15m//s^(2) re...

in the given figure, `alpha=15m//s^(2)` represents the total accleration of a particle moving in the clockwise direction on a circle radius R = 2.5m aat a given of time The speed of the particle is

A

4.5m/s

B

5.0m/s

C

5.7m/s

D

6.2 m/s

Text Solution

Verified by Experts

The correct Answer is:
C
`Tantheta=(dv//dt)/(V^(2)//R)`
`Tan30^(@)=(1)/(sqrt(3))=(dV//dt)/(V^(2)//R)`
`(dV)/(dt)=(1)/(sqrt(3))xx(V^(2))/(R)`
`a=15=sqrt(((dV)/(dt))^(2)+((V^(2))/(R))^(2))` ltBrgt `15=sqrt((4)/(3)((V^(2))/(R))^(2))`
`15=(2)/(sqrt(3))((V^(2))/(R))=(2)/(sqrt(3))xx(V^(2))/(2.5)impliesV^(2)=(15xxsqrt(3)xx2.5)/(2)=32.476=5.7m//s`
Promotional Banner

Similar Questions

Explore conceptually related problems

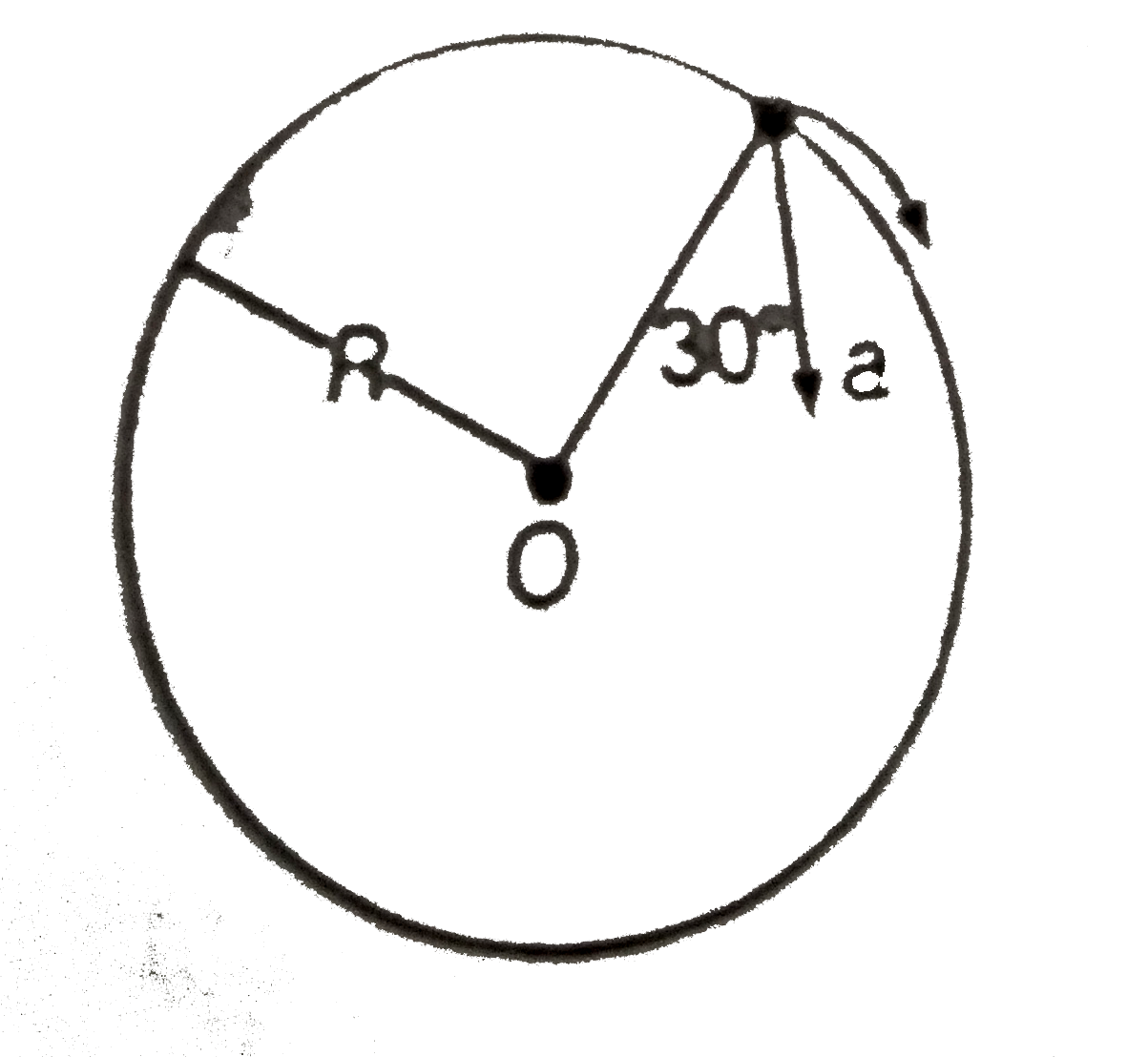
In the given figure, a=15m//s^(2) represents the total acceleration of a particle moving in the clockwise direction in a circle of radius R=2.5m at a given instant of time. The speed of the particle is.

The figure shows the total acceleration a = 32 m s^(-2) of a moving particle moving clockwise in a circle of radius R = 1 m . What are the centripetal acceleration a and speed of the particle at the given instant ?

Centripetal acceleration of a particle of mass m moving in a circle of radius r is 4//r^(2) . What is the angular momentum of the particle ?

Figur shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5m at a given instant of time. At this instant, find: (a) the radius acceleration, (b) the speed of the acceleration, (c) its tangential acceleration.

Figure shows the direction of the total acceleration and velocity of a particle moving clockwise in a circle radius m at an instant of time. Tangential acceleration this instant is 5m//s^(2) . Which of the following statements is not correct?

If a particle moves in a circle of radius 4m at speed given by v=2t at t=4 sec, Total Acceleration of the particle will be:

A particle moves in a circle of radius 5 cm with constant speed and time period 0.2pis . The acceleration of the particle is

A particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is

A particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then

The co-ordinates of a moving particle at any time t are given by x=ct^(2) and y=bt^(2) The speed of the particle is