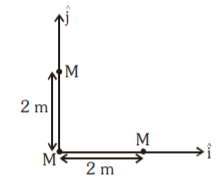
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Three identical spheres each of mass M are placed at corners of right ...
Text Solution
|
- The perpendicular bisector of the three sides of a right - angled t...
Text Solution
|
- Three identical spheres of mass M each are placed at the corners of an...
Text Solution
|
- Four identical spheres each of mass m are placed at the corner of squa...
Text Solution
|
- द्रव्यमान m के तीन आदर्श गोले, 2 मी भुजा वाले एक समबाहु त्रिभुज के कोन...
Text Solution
|
- Three identical spheres each of mass M are placed at corners of right ...
Text Solution
|
- Three equal masses m are placed at the three corners of an equilateral...
Text Solution
|
- Three identical spheres , each of mass M , are placed at the corners o...
Text Solution
|
- Four identical spheres each of mass m are placed at the corner of squa...
Text Solution
|