Home
Class 12
MATHS
ax^2 + bx + c = 0(a > 0), has two roots ...

`ax^2 + bx + c = 0(a > 0),` has two roots `alpha and beta` such `alpha < -2 and beta > 2,` then

A

`4a-2|b|+clt0`

B

`9a-3|b|+clt0`

C

`a-|b|+clt0`

D

`clt0,b^(2)-4acgt0`

Text Solution

Verified by Experts

The correct Answer is:
A, C, D
Here `D gt 0`

`b^(2)-4acgt0`
or `b^(2)gt4ac`…… i and `f(0)lt0`
`impliesclt0`..ii
`f(1)lt0`
`impliesa+b+clt0`………iii
`f(-1)lt0`
`impliesa-b+clt0`………..iv
`f(2)lt0`
`implies4a+2b+clt0`………v
`f(-2)lt0`
`implies4a-2b+clt0`...............vi
From Eqs i and ii we get
`clt0,b^(2)-4acgt0`
From Eqs. (iii) and (iv) we get
`a-|b|+clt0`
and from Eqs (v) and (vi) we get
`4a-2|b|+clt0`
Promotional Banner

Topper's Solved these Questions

  • THEORY OF EQUATIONS

    ARIHANT MATHS ENGLISH|Exercise Exercise (Passage Based Questions)|21 Videos

  • THEORY OF EQUATIONS

    ARIHANT MATHS ENGLISH|Exercise Exercise (Single Integer Answer Type Questions)|10 Videos

  • THEORY OF EQUATIONS

    ARIHANT MATHS ENGLISH|Exercise SCQ_TYPE|1 Videos

  • THE STRAIGHT LINES

    ARIHANT MATHS ENGLISH|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|17 Videos

  • THREE DIMENSIONAL COORDINATE SYSTEM

    ARIHANT MATHS ENGLISH|Exercise Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam|2 Videos

Similar Questions

Explore conceptually related problems

Let a,b,c in R and a gt 0 . If the quadratic equation ax^(2) +bx +c=0 has two real roots alpha and beta such that alpha gt -1 and beta gt 1 , then show that 1 + |b/a| + c/a gt 0

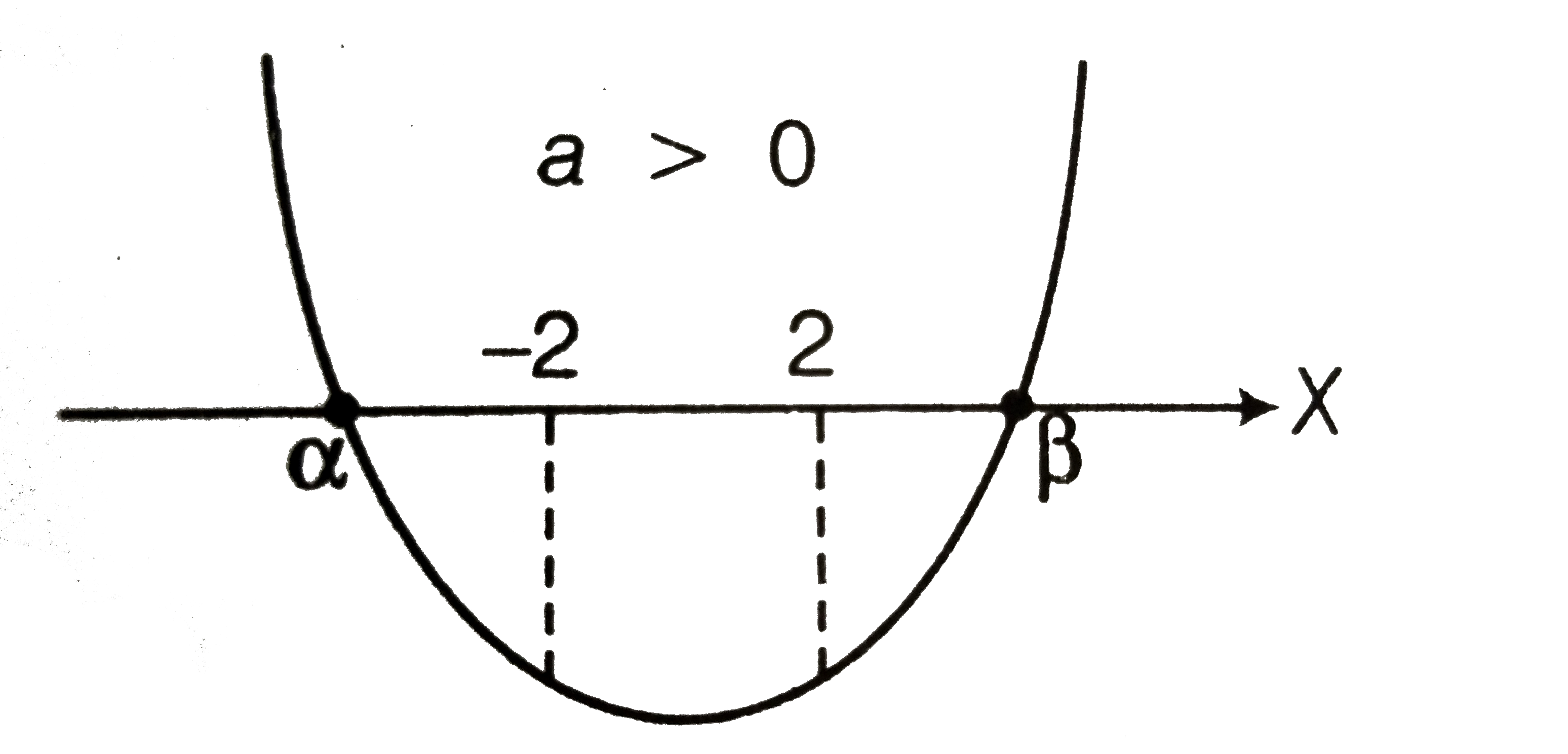
If a ne 0 and the equation ax ^(2)+bx+c=0 has two roots alpha and beta such thet alpha lt -3 and beta gt 2. Which of the following is always true ?

If a, b, c are real if ax^(2)+ bx + c = 0 has two real roots alpha, beta where a lt -1, beta gt 1 then

If alpha, beta are roots of the equation ax^2 + bx + c = 0 then the equation whose roots are 2alpha + 3beta and 3alpha + 2beta is

Consider a quadratic equation ax^2 + bx + c = 0 having roots alpha, beta . If 4a + 2b + c > 0,a-b+c 0 then |[alpha] + [beta]| can be {where [] is greatest integer}

Statement-1: If alpha and beta are real roots of the quadratic equations ax^(2) + bx + c = 0 and -ax^(2) + bx + c = 0 , then (a)/(2) x^(2) + bx + c = 0 has a real root between alpha and beta Statement-2: If f(x) is a real polynomial and x_(1), x_(2) in R such that f(x_(1)) f_(x_(2)) lt 0 , then f(x) = 0 has at leat one real root between x_(1) and x_(2) .

IF alpha , beta are the roots of the equation ax^2+ bx +c=0 then the quadratic equation whose roots are alpha + beta , alpha beta is

In the quadratic equation ax^2 + bx + c = 0 , if Delta = b^2-4ac and alpha + beta, alpha^2 + beta^2, alpha^3 + beta^3 are in GP. where alpha, beta are the roots of ax^2 + bx + c =0 , then

If alpha, beta are the roots of the quadratic equation x^2 + bx - c = 0 , the equation whose roots are b and c , is a. x^(2)+alpha x- beta=0 b. x^(2)-[(alpha +beta)+alpha beta]x-alpha beta( alpha+beta)=0 c. x^(2)+[(alpha + beta)+alpha beta]x+alpha beta(alpha + beta)=0 d. x^(2)+[(alpha +beta)+alpha beta)]x -alpha beta(alpha +beta)=0

Statement-1 : Let a quadratic equation has a root 3 - 9i then the sum of roots is 6. and Statement -2 : If one root of ax^(2) +bx +c=0 ,ane 0, a,b,c in R " is "alpha+ ibeta, alpha,beta in R then the other roots must be alpha-ibeta