Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
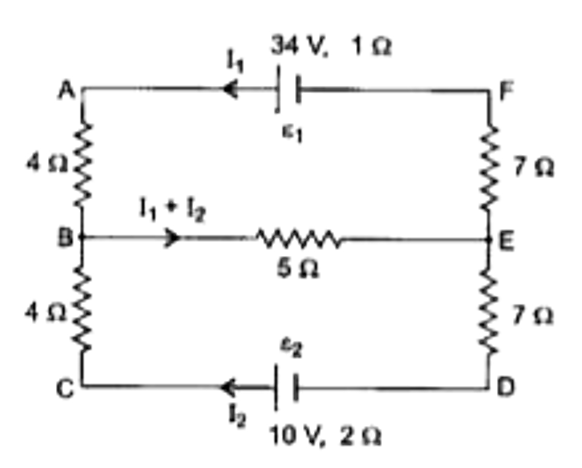
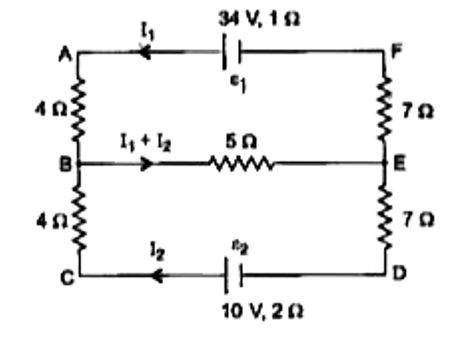
- epsi(1) and epsi(2) are two batteries having e.m.f of 34V and 10V resp...
Text Solution
|
- A battery of emf epsilon and internal resistance r sends currents I(1)...
Text Solution
|
- Using Kirchoff's laws in the electrical net work shown in figure, calc...
Text Solution
|
- A network of resistors is connected to a battery of negligible interna...
Text Solution
|
- find the emf (epsi(0)) and internal resistance (r(0)) if a battery whi...
Text Solution
|
- In the circuit shown in figure. Find the currents I,I(1),I(2) and I(3)...
Text Solution
|
- Two batteries of emf epsi(1) and epsi(2)(epsi(2) gt epsi(1)) and inter...
Text Solution
|
- A 5 V battery with internal resistance 2Omega and a 2V battery with i...
Text Solution
|
- Calculate the values of currents · I(1)I(2)I(3) and I(4) Is and loin t...
Text Solution
|