Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ICSE-MID-POINT THEOREM-4 MARKS QUESTION
- Prove that the figure obtained by joining the mid-points of the adjace...
Text Solution
|
- The diagonals of a quadrilateral intersect at right angles. Prove that...
Text Solution
|
- L and M are the mid-points of sides AB and DC respectively of parallel...
Text Solution
|
- ABCD is a rectangle and P, Q, R and S are mid-points of the sides A...
Text Solution
|
- A parallelogram ABCD has P the mid-point of DC and Q a midpoint of AC ...
Text Solution
|
- D and F are the mid-points of sides AB and AC of a triangle ABC. A lin...
Text Solution
|
- D and F are the mid-points of sides AB and AC of a triangle ABC. A lin...
Text Solution
|
- In the figure, given below, 2AD=AB,P is the mid-point of AB, Q is the ...
Text Solution
|
- In the figure, given below, 2AD=AB,P is the mid-point of AB, Q is the ...
Text Solution
|
- In parallelogram ABCD, E and F are mid-points of the sides AB and CD r...
Text Solution
|
- In parallelogram ABCD, E and F are mid-points of the sides AB and CD r...
Text Solution
|
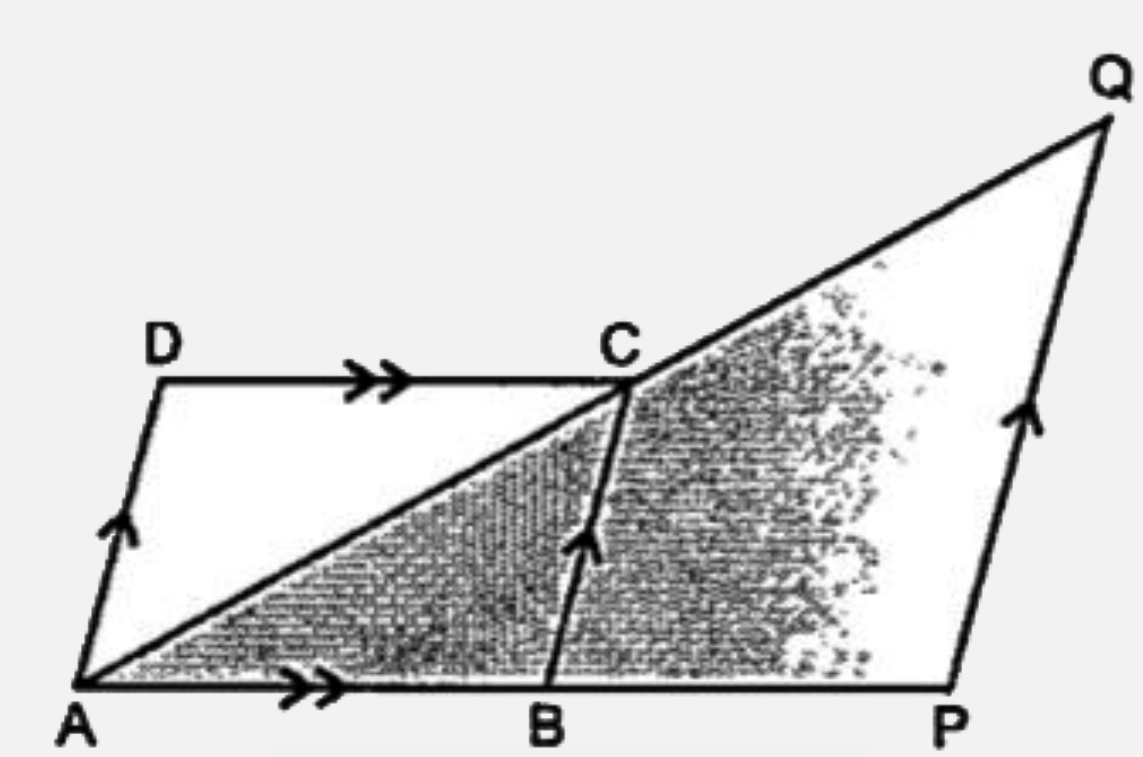
- In the given figure, ABCD is a parallelogram. AB is produced to P, suc...
Text Solution
|
- In the given figure, ABCD is a parallelogram. AB is produced to P, suc...
Text Solution
|
- In the given figure ABCD is a trapezium, P is the mid-point of side AD...
Text Solution
|
- In the given figure ABCD is a trapezium, P is the mid-point of side AD...
Text Solution
|