Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ICSE-RECTILINEAR FIGURES-QUADRILATERALS AND ITS PROPERTIES - 4 MARKS QUESTIONS
- The given figure shows a square ABCD and an equilateral triangle ABP. ...
Text Solution
|
- In the given figure, ABCD is a rhombus with angle A = 67^(@). If ...
Text Solution
|
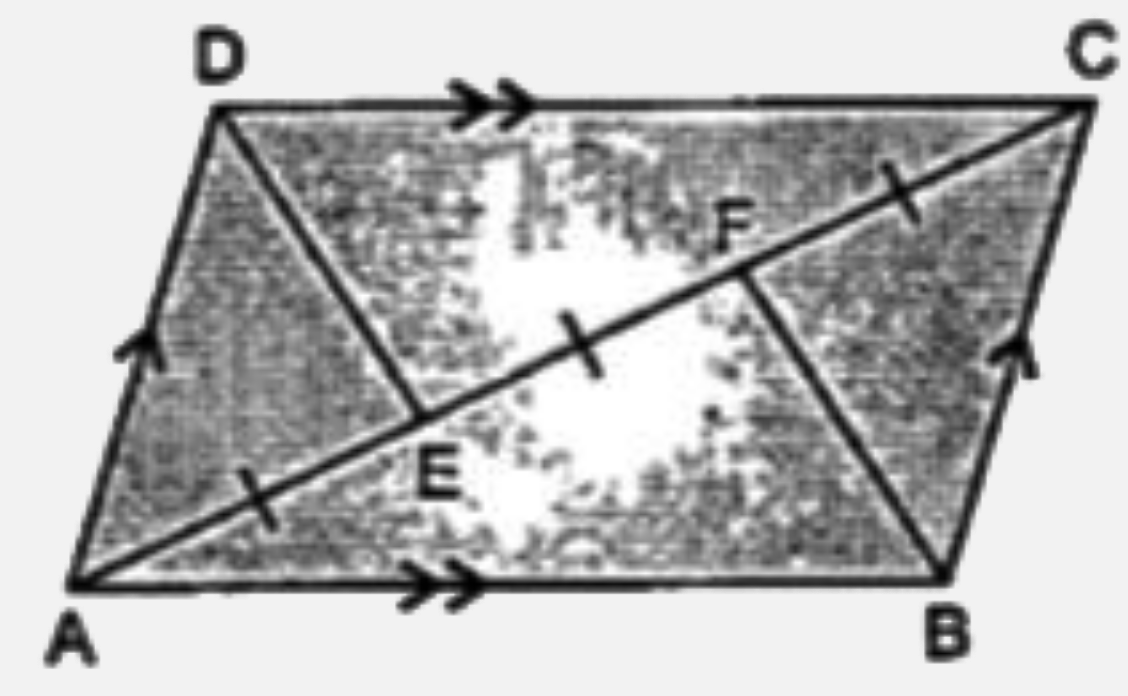
- The along side figure shows a parallelogram ABCD in which AE = EF = FC...
Text Solution
|
- The bisectors of the angle of a parallelogram enclose a parallelogr...
Text Solution
|
- In parallelogram ABCD, the bisector of angle A meets DC at P and AB = ...
Text Solution
|
- In a quadrilateral ABCD, AB = AD and CB = CD. Prove that : (i) AC bi...
Text Solution
|
- The following figure shows a trapezium ABCD in which AB is parallel to...
Text Solution
|