Home
Class 11
PHYSICS
A steel wire of diameter 0.8 mm and leng...

A steel wire of diameter 0.8 mm and length 1m is clamped firmly at two points P and Q which are one metre apart and in the same horizontal plane. A body is hung from the middle point of the wire, such that the middle point sags one cm lower from the original position as shown in figure. Calculate the mass of the body. `Y = 2xx 10^(11) N//m^(2)`.

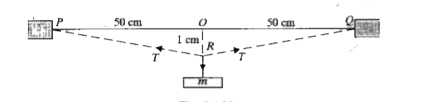
Text Solution

Verified by Experts

Let T be the tension in each segment of the wire and `/_ ORQ = /_ ORP = theta`
`2T cos theta = mg `
Stress `= ( T)/( A)`, T = Stress `xxA`
`T = Y xx` Strain `xx `A
`A = pi d^(2) //4`
From the triangle POR, `PR = sqrt( PO^(2) + OR^(2)) = sqrt(2500 +1) = 50.01 `cm
Final length of the wire ` = 50.01 + 50.01 = 100.02cm`
Original length `= 100cm`
Change in length = 0.02cm
Strain `= ( 0.02)/( 100) = 2 xx 10^(-4)`
`T = Y xx ` Strain `xx A`
`= 2xx 10^(11) xx 2 xx 10^(-4) xx 3.14 xx (( 0.8xx 10^(-3))^(2))/( 4)`
= 20.096N
`m = ( 2T cos theta )/( g) =( 2 xx 20.096 xx 1)/(9.8 xx 50.01 ) = 0.082 kg`
Promotional Banner

Topper's Solved these Questions

  • PROPERTIES OF MATTER

    ICSE|Exercise MODULE 2 (SOLVED EXAMPLES)|22 Videos

  • PROPERTIES OF MATTER

    ICSE|Exercise MODULE 3 (SOLVED EXAMPLES)|31 Videos

  • OSCILLATIONS

    ICSE|Exercise SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)|2 Videos

  • SAMPLE QUESTION PAPER - 01

    ICSE|Exercise SECTION - D|12 Videos

Similar Questions

Explore conceptually related problems

The moment of inertia of a uniform rod of mass 0.50 kg and length 1 m is 0.10 kg m^2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.

A steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is x. Strain in the wire is proportional to

A steel wire of original length 1 m and cross-sectional area 4.00 mm^2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16 kg is suspended from the middle point of the wire, what would be its vertical depression ? Y of the steel =2.0xx10^11Nm^-2 . Take g=10 ms^-2

A steel wire of negligible mass, length 2I , cross sectional area 'A' and Young's modulus 'Y' is held between two rigid walls. A small body of mass 'm' is suspended from its middle point 'O' as shown. The vertical descent of the middle point 'O' of the wire is

A wire of cross section A is stretched horizontally between two clamps located 2l m apart. A weight W kg is suspended from the mid-point of the wire. If the mid-point sags vertically through a distance x lt l , the strain produced is

A steel wire of mass mu per unit length with a circular cross-section has a radius of 0.1cm . The wire is of length 10m when measured lying horizontal, and hangs from a hook on the wall. A mass fo 25kg is hung from the free end of the wire. Assume the wire to be uniform and laterla strain lt lt logitudinal strain. If density of steel is 7860 kg m^(-3) and Young's modulus is 2xx10^(11) N//m^(2) then the extension in the length fo the wire is

A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of 2 rev.//s at the bottom of the circle. The cross-sectional area of the wire is 0.065 cm^(2) . Calculate the elongaton of the wire when the mass is at the lowest point of its path Y_(steel) = 2 xx 10^(11) Nm^(-2) .

A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of 2 rev.//s at the bottom of the circle. The cross-sectional area of the wire is 0.065 cm^(2) . Calculate the elongation of the wire when the mass is at the lowest point of its path Y_(steel) = 2 xx 10^(11) Nm^(-2) .

Find the net vertical displacement of point O, when a mass of 2.5 kg is suspended from the mid-point O of the rod shown (Y=2xx10^(11)N//m^(2)) .

A sphere of radius 10 cm and mass 25 kg is attached to the lower end of a steel wire of length 5 m and diameter 4 mm which is suspended from the ceiling of a room . The point of support is 521 cm above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position (Y_(steel) = 2xx10^(11) N//m^(2)) .