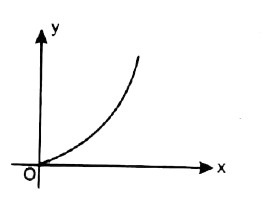
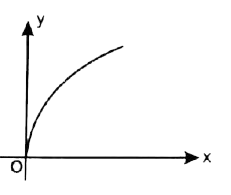
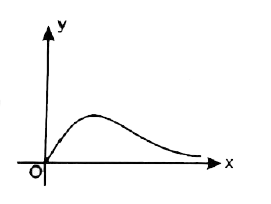
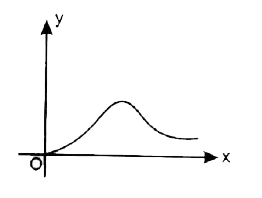
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
APPLICATION OF DERIVATIVES
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (ONE OR MORE THAN ANSWER IS/ARE CORRECT )|29 VideosAPPLICATION OF DERIVATIVES
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (COMPREHENSION TYPE PROBLEMS)|15 VideosAREA UNDER CURVES
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise AXERCISE (SUBJECTIVE TYPE PROBLEMS)|8 Videos
Similar Questions
Explore conceptually related problems
VIKAS GUPTA (BLACK BOOK) ENGLISH-APPLICATION OF DERIVATIVES -EXERCISE (SUBJECTIVE TYPE PROBLEMS)
- Which of the following graph represent the function f (x) = int (0) ^(...
Text Solution
|
- A conical vessel is to be prepared out of a circular sheet of gold of ...
Text Solution
|
- On [1,e], then least and greatest vlaues of f (x) = x^(2)ln x are m a...
Text Solution
|
- If f (x)= (px)/(e ^(x)) - (x ^(2))/(2) + x is a decreasing function f...
Text Solution
|
- L e tf(x)={x e^(a x),xlt=0x+a x^2-x^3,x >0 where a is a positive cons...
Text Solution
|
- Find sum of all possible values of the real parameter 'b' if the diffe...
Text Solution
|
- Let 'theta' be the angle in radians between the curves (x ^(2))/(36) +...
Text Solution
|
- Let set of all possible values of lamda such that f (x)= e ^(2x) - (la...
Text Solution
|
- Let a,b,c and d be non-negative real number such that a ^(5)+b^(5) le ...
Text Solution
|
- There is a point (p,q) on the graph of f(x)=x^(2) and a point (r,s) on...
Text Solution
|
- If f(x)=max| 2 siny-x|, (where y in R), then find the minimum value o...
Text Solution
|
- Let f (x) = int (0)^(x) ((a -1) (t ^(2)+t+1)^(2) -(a+1)(t^(4)+t ^(2) +...
Text Solution
|
- The numbr of real roots of the equation x ^(2013)+ e ^(2014x) =0 is
Text Solution
|
- Let the maximum value of expression y= (x ^(4)-x ^(2))/(x ^(6) + 2x ^(...
Text Solution
|
- The least positive integral value of 'k' for which there exists at lea...
Text Solution
|
- The coordinates of a particle moving in a plane are given by x (t) = a...
Text Solution
|
- A tank contains 100 litres of fresh water. A solution containing 1 gm/...
Text Solution
|
- If f (x) is continous and differentiable in [-3,9] and f'(x) in [-2,8]...
Text Solution
|
- It is given that f (x) is defined on R satisfying f (1)=1 and for AA ...
Text Solution
|
- The number of normals to the curve 3y ^(3) =4x which passes through th...
Text Solution
|
- Find the number of real root (s) of the equation ae ^(x) =1+ x + (x ^(...
Text Solution
|