Home
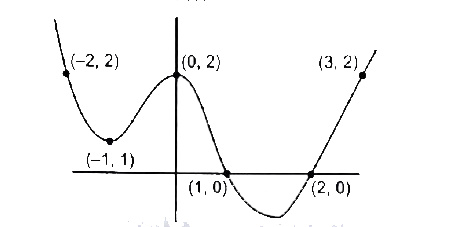
Class 12
MATHS
In the given figure graph of : y =p (x...

In the given figure graph of :
`y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ ….. + a _(n)` is given.

The product of all imaginary roots of `p(x) =0` is:

A

`-2`

B

`-1`

C

`-1//2`

D

noen of these

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • APPLICATION OF DERIVATIVES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (MATHCING TYPE PROBLEMS)|6 Videos

  • APPLICATION OF DERIVATIVES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (SUBJECTIVE TYPE PROBLEMS)|22 Videos

  • APPLICATION OF DERIVATIVES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (ONE OR MORE THAN ANSWER IS/ARE CORRECT )|29 Videos

  • AREA UNDER CURVES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise AXERCISE (SUBJECTIVE TYPE PROBLEMS)|8 Videos

Similar Questions

Explore conceptually related problems

In the given figure graph of : y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ …..+ a _(n) is given. The minimum number of real roots of equation (p' (x))^(2) +p(x)p''(x) =0 are:

In the given figure graph of : y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ …..+ a _(n) is given. If p (x) + k=0 has 4 distinct real roots alpha, beta, gamma,delta then [alpha]+[beta]+[gamma]+[delta], (where [.] denotes greatest integer function) is equal to:

In the given figure graph of y=p(x)=x^(4)+ax^(3)+bx^(2)+cx+d is given The product of all imaginary roots of p(x)=0 is (a) 1 (b) 2 (c) 1/3 (d) 1/4

Differentiate |x|+a_(0)x^(n)+a_(1)x^(n-1)+a_(2)x^(n-1)+...+a_(n-1)x+a_(n)

Differentiate the following with respect of x : a_0x^n+a_1x^(n-1)+a_2x^(n-2)++a_(n-1)x+a_ndot

If (1 + x + x^(2) + x^(3))^(n) = a_(0) + a_(1)x + a_(2)x^(2)+"……….."a_(3n)x^(3n) then which of following are correct

Let n be positive integer such that, (1+x+x^(2))^(n)=a_(0)+a_(1)x+a_(2)x^(2)+….+a_(2n)x^(2n) , then a_(r) is :

If (1+2x+x^(2))^(n) = sum_(r=0)^(2n)a_(r)x^(r) , then a_(r) =

Find a_(1) and a_(9) if a_(n) is given by a_(n) = (n^(2))/(n+1)

Let (1 + x^(2))^(2) (1 + x)^(n) = a_(0) + a_(1) x + a_(2) x^(2) + … if a_(1),a_(2) " and " a_(3) are in A.P , the value of n is