Home
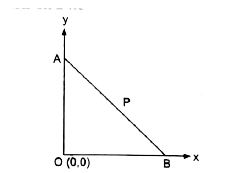
Class 12
MATHS
A rod of AB of length 3 rests on a wall ...

A rod of AB of length 3 rests on a wall as follows :

P is a point on AB such that ` AP : PB = 1 : 2 ` If the rod slides along the wall, then the locus of P lies on

A

`2x + y + xy = 2 `

B

` 4x^(2) + xy + xy + y^(2) = 4`

C

` 4x^(2) + y^(2) =4 `

D

` x^(2) + y^(2) - x - 2y =0`

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise-2 : One or More than One Answer is/are Correct|12 Videos

  • STRAIGHT LINES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise-3 : Comprehension Type Problems|4 Videos

  • SOLUTION OF TRIANGLES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise-5 : Subjective Type Problems|11 Videos

  • TRIGONOMETRIC EQUATIONS

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise-5 : Subjective Type Problems|9 Videos

Similar Questions

Explore conceptually related problems

ABCD is a parallelogram of area 162 sq. Cm P is a point on AB such that AP : PB = 1 :2 Calculate The area of Delta APD

ABCD is a parallelogram of area 162 sq. Cm P is a point on AB such that AP : PB = 1 :2 Calculate The ratio of PA : DC.

A(1, 4) and B (4, 8) are two points. P is a point on AB such that AP=AB+BP . If AP=10 , find the coordinates of P .

If A=(2, -3, 7), B = (-1, 4, -5) and P is a point on the line AB such that AP : BP = 3 : 2 then P has the coordinates

The given figure shows a parallelogram ABCD with area 324sq. cm. P is a point in AB such that AP:PB= 1:2 . Find the area of DeltaAPD .

In the given figure, P is a point on AB such that AP : PB = 4: 3 . PQ is parallel to AC. Calculate the ratio PQ : AC, giving reason for your answer.

A rod A B of length 15c m rests in between two coordinate axes in such a way that the end point A lies on x- axis and end point B lies on y -axis . A point is taken on the rod in such a way that A P=6c m . Show that the locus of P is an ellipse. Also find its eccentricity.

A rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m//s along the wall. Find the velocity of end B, when end B makes 30^(@) with wall PQ.

AB is a line of fixed length, 6 units, joining the points A (t, 0) and B which lies on the positive y-axis. P is a point on AB distant 2 units from A. Express the co-ordinates of B and P in terms of t. Find the locus of P as t varies.

AB is a chord of the circle x^2 + y^2 = 25/2 .P is a point such that PA = 4, PB = 3. If AB = 5, then distance of P from origin can be: