Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SOLUTION OF TRIANGLES
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise-4 : Matching Type Problems|2 VideosSEQUENCE AND SERIES
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (SUBJECTIVE TYPE PROBLEMS)|21 VideosSTRAIGHT LINES
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise-5 : Subjective Type Problems|10 Videos
Similar Questions
Explore conceptually related problems
VIKAS GUPTA (BLACK BOOK) ENGLISH-SOLUTION OF TRIANGLES-Exercise-5 : Subjective Type Problems
- If the median AD of triangle ABC makes an angle pi/4 with the side BC,...
Text Solution
|
- In parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2...
Text Solution
|
- In a DeltaABC, inscribed circle with centre I touches side AB, AC and ...
Text Solution
|
- If Delta be area of incircle of a triangle ABC and Delta1,Delta2,Delt...
Text Solution
|
- In Delta ABC, P is an interior point such that angle PAB = 10^(@), ang...
Text Solution
|
- In an acute angled triangle ABC, angleA=20^(@), let DEF be the feet of...
Text Solution
|
- If the quadratic equation ax^2+bx+c=0 has equal roots where a, b, c d...
Text Solution
|
- If in the triangle ABC, "tan"(A)/(2), "tan"(B)/(2) and "tan"(C )/(2) a...
Text Solution
|
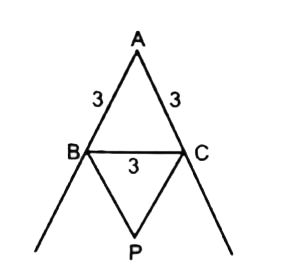
- Sides AB and AC in an equilateral triangle ABC with side length 3 is ...
Text Solution
|
- Let a, b, c be sides of a triangle ABC and Delta denotes its area . ...
Text Solution
|
- Circumradius of DeltaABC is 3 cm and its area is 6 cm^(2). If DEF is t...
Text Solution
|