Home
Class 12
MATHS
A rod AB of length 2L and mass m is lyin...

A rod `AB` of length `2L` and mass `m` is lying on a horizontal frictionless surface. A particle of same mass `m` travelling along the surface hits the rod at distance `(L)/(2)` from `COM` with a velocity `v_(0)` in a direction perpendicular to rod and sticks to it.

Distance of point `P` on rod from `B` which is at rest immediately afte collision is

Text Solution

Verified by Experts

The correct Answer is:
5
Promotional Banner

Topper's Solved these Questions

  • VECTOR & 3DIMENSIONAL GEOMETRY

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise-4 : Matching Type Problems|2 Videos

  • TRIGONOMETRIC EQUATIONS

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise-5 : Subjective Type Problems|9 Videos

Similar Questions

Explore conceptually related problems

A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance (L)/(2) from COM with a velocity v_(0) in a direction perpendicular to rod and sticks to it. Angular velocity of rod just after collision is

A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance (L)/(2) from COM with a velocity v_(0) in a direction perpendicular to rod and sticks to it. Angular velocity of rod just after collision is

A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v_(0) in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest (a). Find the ratio m//M (b). A point P on the rod is at rest immediately after collision find the distance AP. (c). Find the linear speed of the point P a time piL//3v_(0) after the collision.

A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v_(0) in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest (a). Find the ratio m//M (b). A point P on the rod is at rest immediately after collision find the distance AP. (c). Fid the linear speed of the point P a time piL//3v_(0) after the collision.

A uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it. Determine the position of the point on the rod which remains stationary immediately after collision.

A homogenous rod of length l=etax and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v_(0) perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v_(0) , then:

A rod CD of length L and mass m is placed horizontally on a frictionless horizontal surface as shown. A second identical rod AB which is also placed horizontally ( perpendicular to CD) on the same horizontal surface is moving along the surface with a velocity v in a direction perpendicular to rod CD and its and B strikes the rod CD at end C and sticks to it rigidity. Then,

A uniform rod of length 8 a and mass 6 m lies on a smooth horizontal surface. Two point masses m and 2 m moving in the same plane with speed 2 v and v respectively strike the rod perpendicular at distances a and 2a from the mid point of the rod in the opposite directions and stick to the rod. The angular velocity of the system immediately after the collision is

A rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37^@ with the rod. The collision is elastic. After collision,

A uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v_0 , hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

VIKAS GUPTA (BLACK BOOK) ENGLISH-VECTOR & 3DIMENSIONAL GEOMETRY-Exercise-5 : Subjective Type Problems
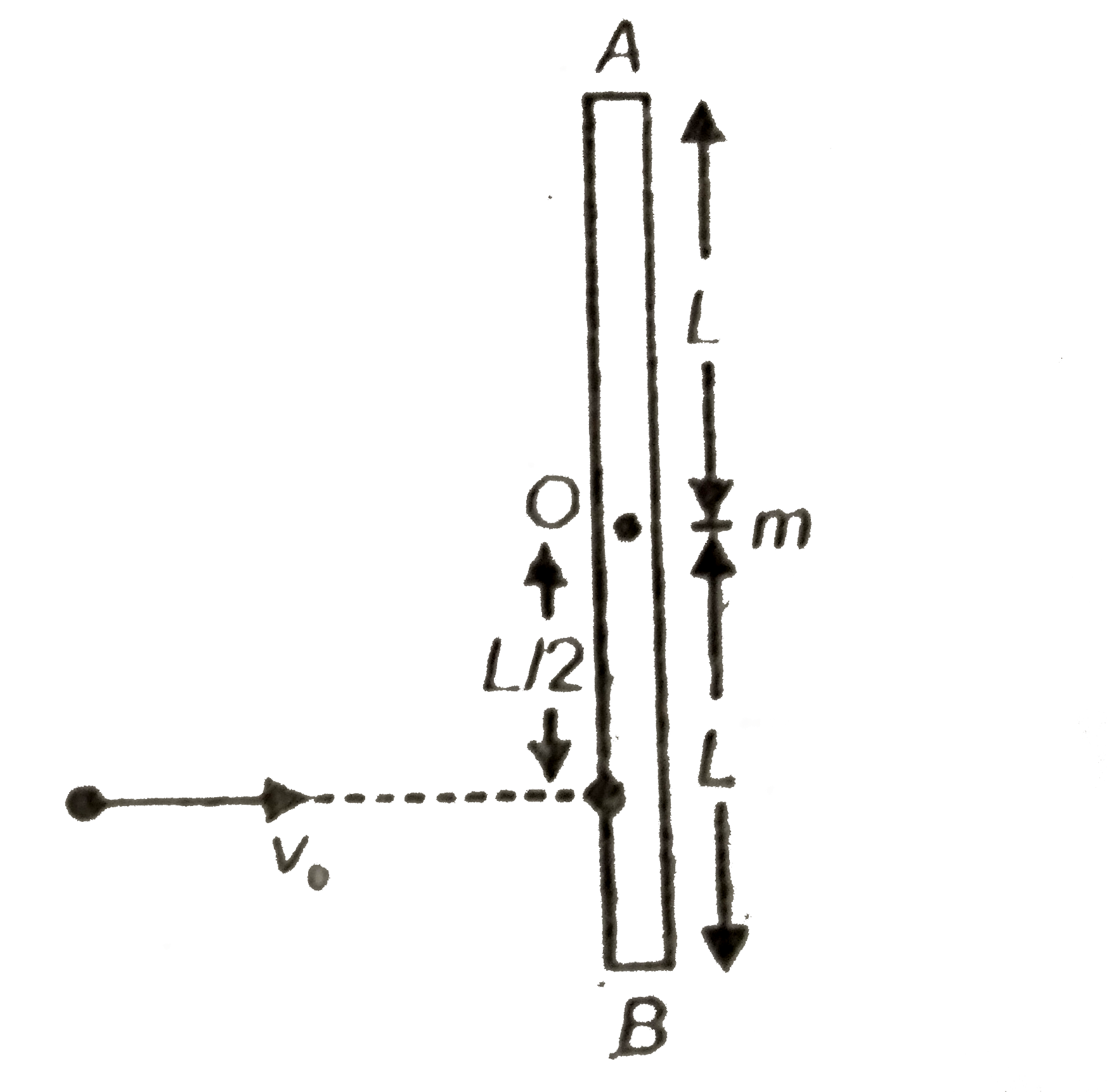
  1. A rod AB of length 2L and mass m is lying on a horizontal frictionless...

    Text Solution

    |

  2. If hata, hatb and hatc are non-coplanar unti vectors such that [hata ...

    Text Solution

    |

  3. Let OABC be a tetrahedron whose edges are of unit length. If vec OA = ...

    Text Solution

    |

  4. If A is the matrix [(1,-3),(-1,1)], then A-(1)/(3)A^(2)+(1)/(9)A^(3)……...

    Text Solution

    |

  5. A sequence of 2xx2 matrices {M(n)} is defined as follows M(n)=[((1)/(...

    Text Solution

    |

  6. Let |veca|=1, |vecb|=1 and |veca+vecb|=sqrt(3). If vec c be a vector ...

    Text Solution

    |

  7. Let vecr=(veca xx vecb)sinx+(vecb xx vec c)cosy+2(vec c xx vec a), whe...

    Text Solution

    |

  8. The plane denoted by P1 : 4x+7y+4z+81=0 is rotated through a right ang...

    Text Solution

    |

  9. ABCD is a regular tetrahedron, A is the origin and B lies on x-axis. A...

    Text Solution

    |

  10. A, B, C, D are four points in the space and satisfy |vec(AB)|=3, |vec(...

    Text Solution

    |

  11. Let OABC be a regular tetrahedron of edge length unity. Its volume be ...

    Text Solution

    |

  12. If veca and vecb are non zero, non collinear vectors and veca(1)=lamb...

    Text Solution

    |

  13. Let P and Q are two points on the curve y=log((1)/(2))(x-0.5)+log2sqrt...

    Text Solution

    |

  14. Let P and Q are two points on the curve y=log((1)/(2))(x-0.5)+log2sqrt...

    Text Solution

    |

  15. If a, b, c, l, m, n in R-{0} such that al+bm+cn=0, bl+cm+an=0, cl+am+b...

    Text Solution

    |

  16. Let vec ua n d vec v be unit vectors such that vec uxx vec v+ vec u=...

    Text Solution

    |