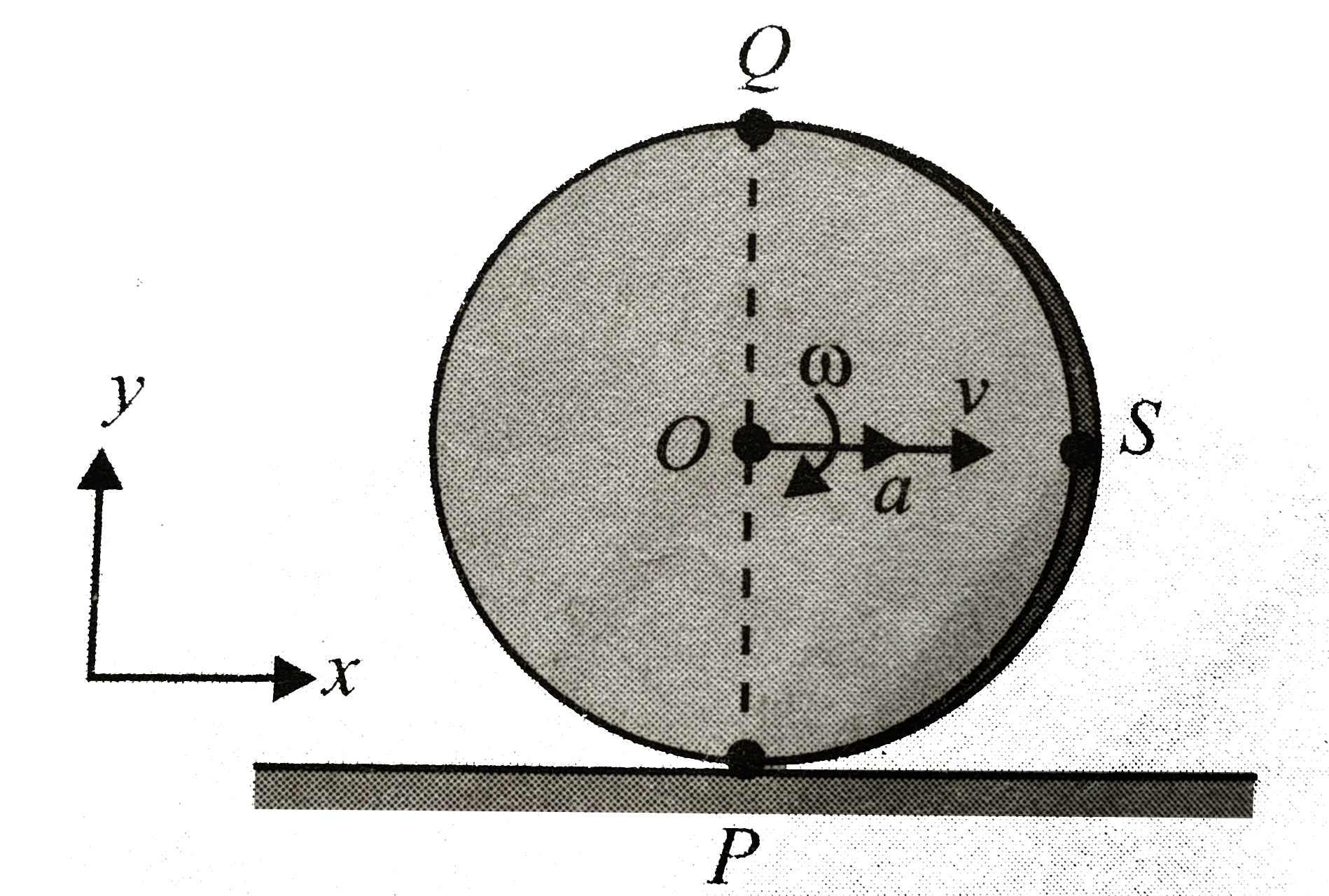Home
Class 11
PHYSICS
Consider a wheel rolls without slipping ...

Consider a wheel rolls without slipping and its centre moves with constant acceleration a. Find the acceleration of points `O,P,Q` and `S` when linear velocity of the centre of wheel is `v`.

Text Solution

Verified by Experts

As body is rolling, we can write the following: Acceleration of cenntre of mass `a=alphaR`
Velocity of centre of mass `v=omegaR`

From fig d. we get the following
Resultant acceleration of point `O, a_(0)=ahati`
Acceleration of `p, a_(P)=ahati-ahati+omega^(2)Rhatj=omega^(2)Rhatj`
Acceleration of `Q, a_(Q)=ahati+ahati-omega^(2)Rhatj=2ahati-omega^(2)Rhatj`
Acceleration of `S, a_(s)=ahati-omega^(2)Rhatj=(a-omega^(2)R)hati-ahatj`
Promotional Banner

Topper's Solved these Questions

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS ENGLISH|Exercise Solved Examples|12 Videos

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS ENGLISH|Exercise Exercise 3.1|11 Videos

  • RIGID BODY DYNAMICS 1

    CENGAGE PHYSICS ENGLISH|Exercise Integer|11 Videos

  • SOUND WAVES AND DOPPLER EFFECT

    CENGAGE PHYSICS ENGLISH|Exercise Integer|16 Videos

Similar Questions

Explore conceptually related problems

A solid sphere of mass m rolls without slipping on an inclined plane of inclination theta . The linear acceleration of the sphere is

The centre of a wheel rolling without slipping on a plane surface moves with a speed v_(0) . A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed

A ring rolls without slipping on the ground. Its centre C moves with a constant speed u.P is any point on the ring. The speed of P with respect to the ground is v .

A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration at

A constant horizontal force of 10 N is applied at the centre of a wheel of mass 10 kg and radius 0.30 m . The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60 m//s^(2) . a. What are the magnitude and direction of the frictional force on the wheel? b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?

A disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in figure. The magnitude of acceleration of point P at an instant when its linear velocity is v and angular velocity is ω will be:

A wheel rotating with uniform acceleration covers 50 rev in the first five second after the start. Find the angular acceleration and the angular velocity at the end of five second.

The wheel of radius R rolls wihtout slipping on horizontal rough surface and its centre O has an acceleration a_(0) in forward direction. A point P on the wheel is a distance r from O and angular position theta from horizontal. Find the angle theta for which point P can have zero acceleration in this position .

When a solid sphere rolls without slipping down an inclined plane making an angle theta with the horizontal, the acceleration of its centre of mass is a . If the same sphere slides without friction, its.

When a solid sphere rolls without slipping down an inclined plane making an angle theta with the horizontal, the acceleration of its centre of mass is a . If the same sphere slides without friction, its.