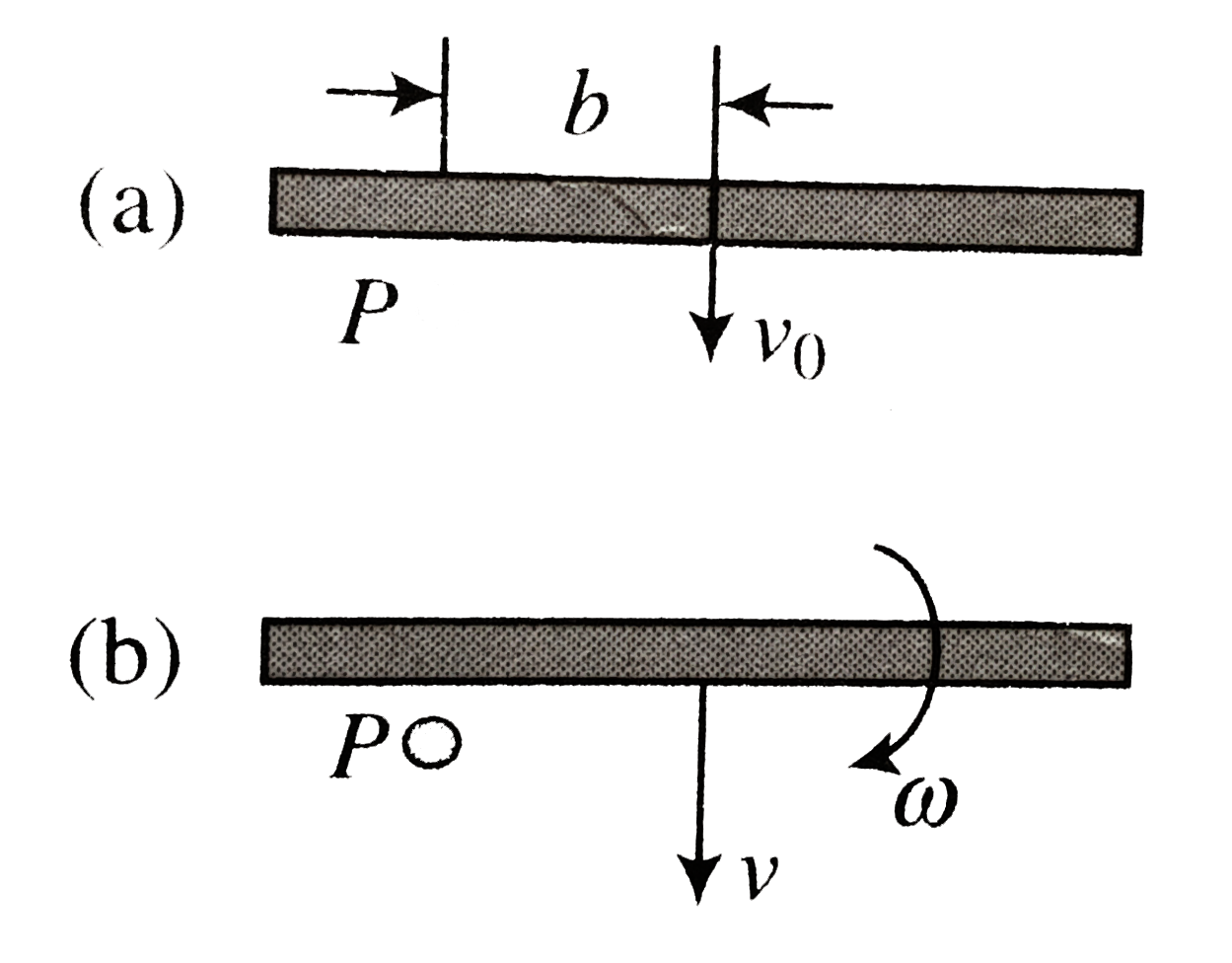
Method 1: At the time of impact the force acting on the rod is `N` (upward) and mg (downward). Since normal reaction is an ampulsive force during impact, `Ngt gtmg`. Then we disregard the effect of gravity during the impact.
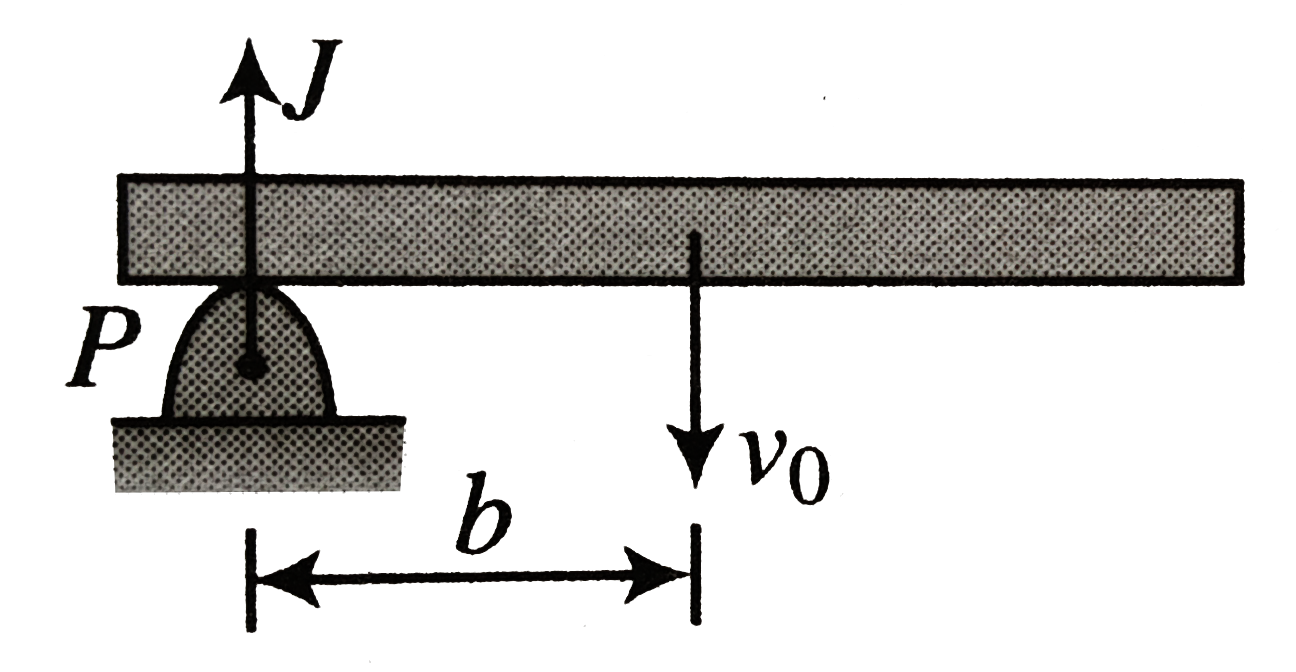
Impulse equation `mv_(0)=J=mv` ..........i
The angular impulse of `N` is `J.b =(ml^(2))/12 omega`
`J=(ml^(2))/(12b)omega`...........ii
Adding eqn i and ii we have
`v_(0)-v=(l^(2)omega)/(12b)`.............iii
Newton's empirical formula gives us
`v_(p)=-v_(0)` ..........iv
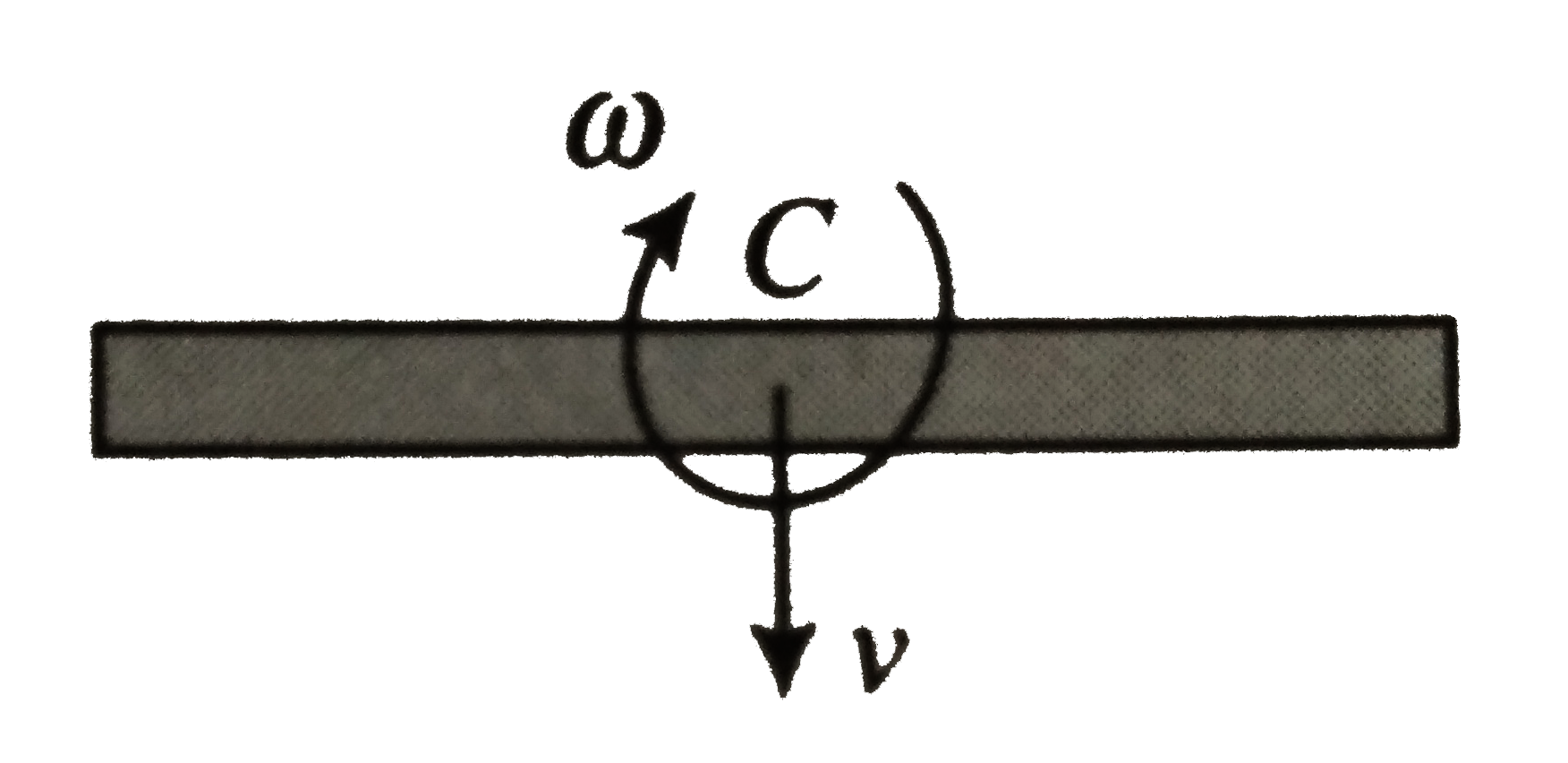
The velocity of `P` is `vecv_(P)=vecv_(PC)+vecv_(C)`
`v-bomega=-ev_(0)`..............v
Now we have two equan ii and iv for two unknowns `v` and `omega`,.
Solving these two equations we have `v=(12b^(2)-el^(2))/(12b^(2)+l^(2))v_(0)`
Method 2: If we choose the fixed point at `P`, the angular impulse about `P` is zero because the impusle `J` passes through `P` during impact.
hence the angular momentum of the rod just before and just after the impact about remain constant.
`vecL_(1)=vecL_(2)`, where `vecL_(1)=mv_(0)b(-hatk)`
and `vecL_(2)=(ml^(2))/12 omega(-hatk)+mvb(-hatk)`
Then `mv_(0)b=mvb+(ml^(2))/12 omega`
This gives `v_(0)-v=(l^(2)omega)/(12b)`
The other equations remain as unchanged. Solving the above eqn we will obtain the same value of `v`.



