Text Solution
Verified by Experts
Topper's Solved these Questions
RIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise Exercise 3.2|13 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise Exercise 3.3|21 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise Solved Examples|12 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS ENGLISH|Exercise Integer|11 VideosSOUND WAVES AND DOPPLER EFFECT
CENGAGE PHYSICS ENGLISH|Exercise Integer|16 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 2-Exercise 3.1
- A uniform spherical shell of mass M and radius R rotates, about a vert...
Text Solution
|
- A uniform rod of mas m and length l is kept vertical with the lower en...
Text Solution
|
- A rigid body is made of three identical thin rods, each with length fa...
Text Solution
|
- The steel balls A and B have a mass of 500 g each and al rotating abou...
Text Solution
|
- A uniform rod smoothly pivoted at one of its ends is released from res...
Text Solution
|
- A composite rod comprising two rods of mass m and 2m and each of lengt...
Text Solution
|
- A rod of mass m spins with an angular speed omega=sqrt(g/l), Find its ...
Text Solution
|
- A uniform disc of mass m is fitted (pivoted smoothly) with a rod of ma...
Text Solution
|
- A uniform rod of length l is from rest such that it rotates about a sm...
Text Solution
|
- A uniform disc of mass M and radius R is pivoted about the horizontal ...
Text Solution
|
- A copper ball of mass m = 1 kg with a radius of r = 10 cm rotates with...
Text Solution
|
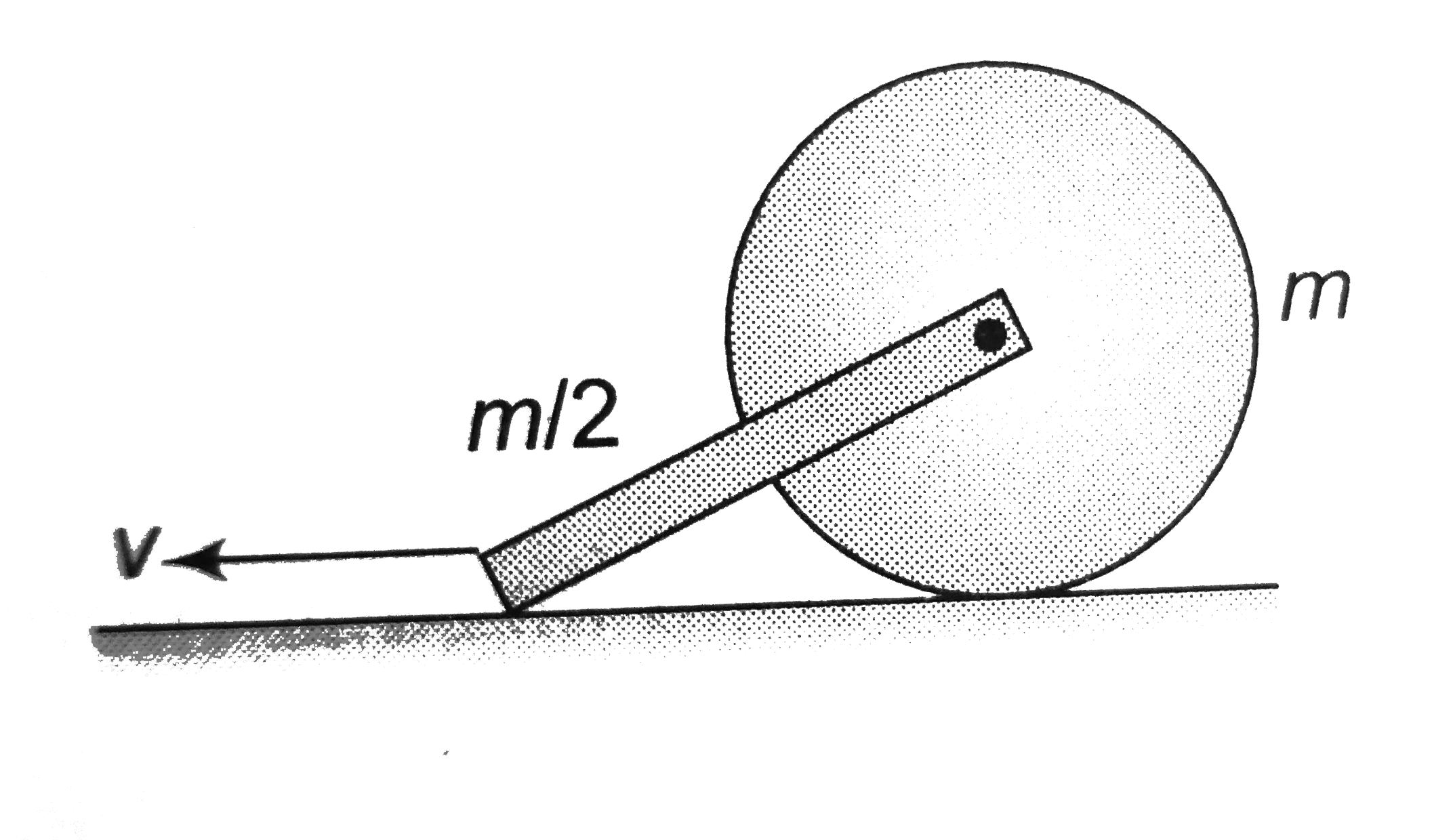 .
.