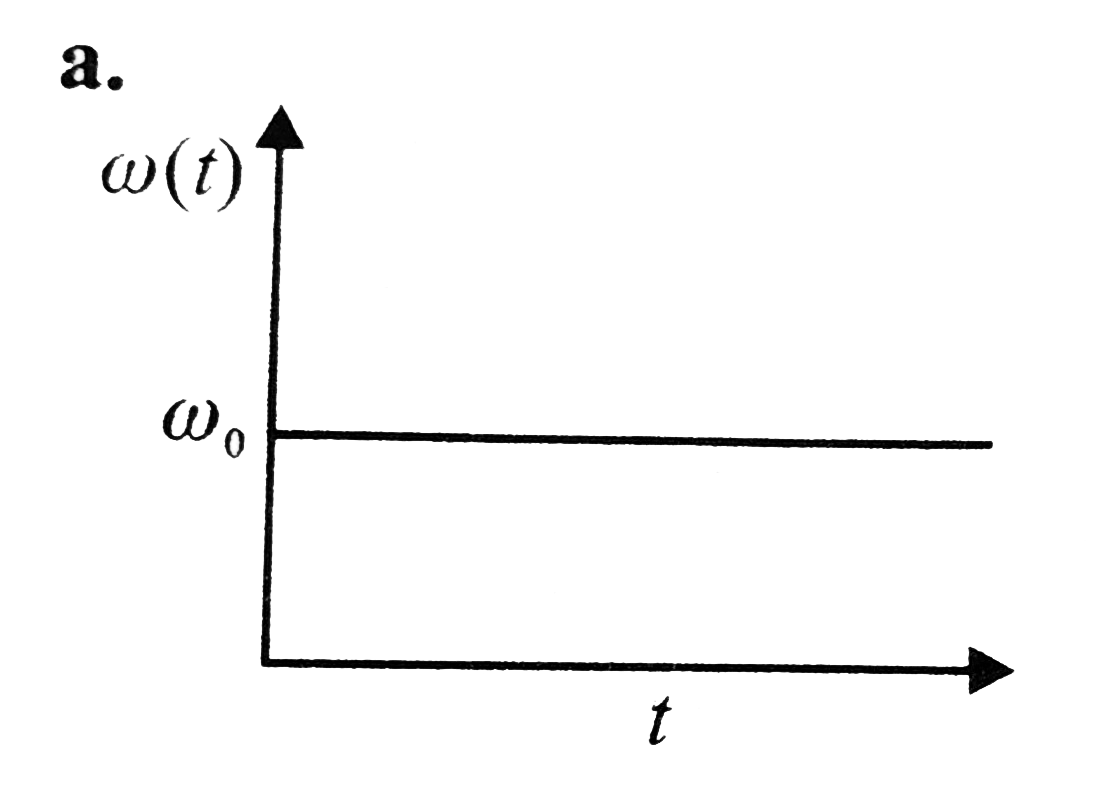
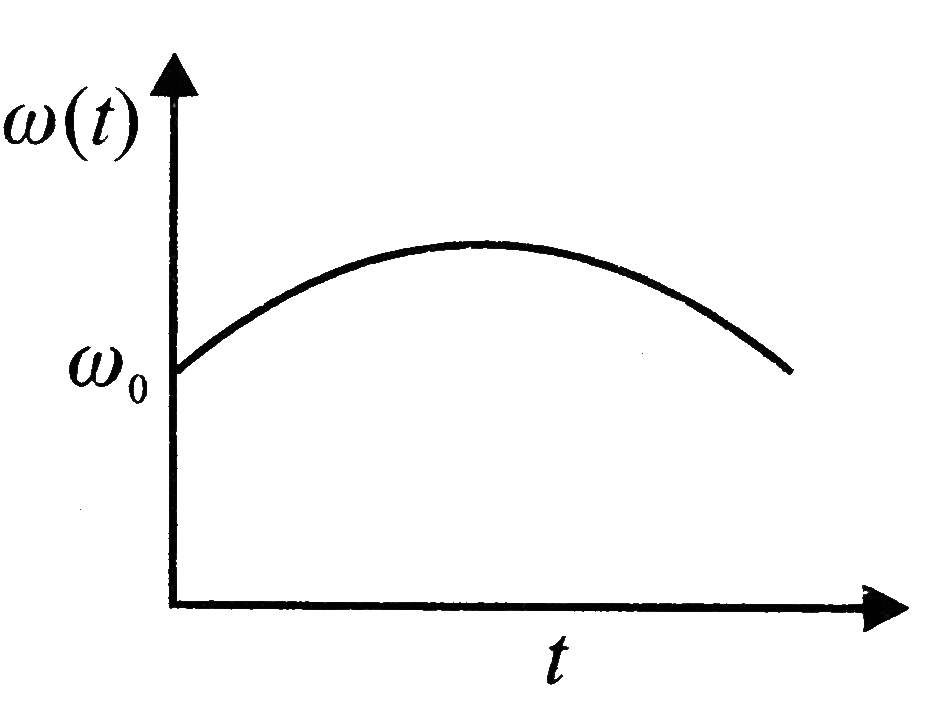
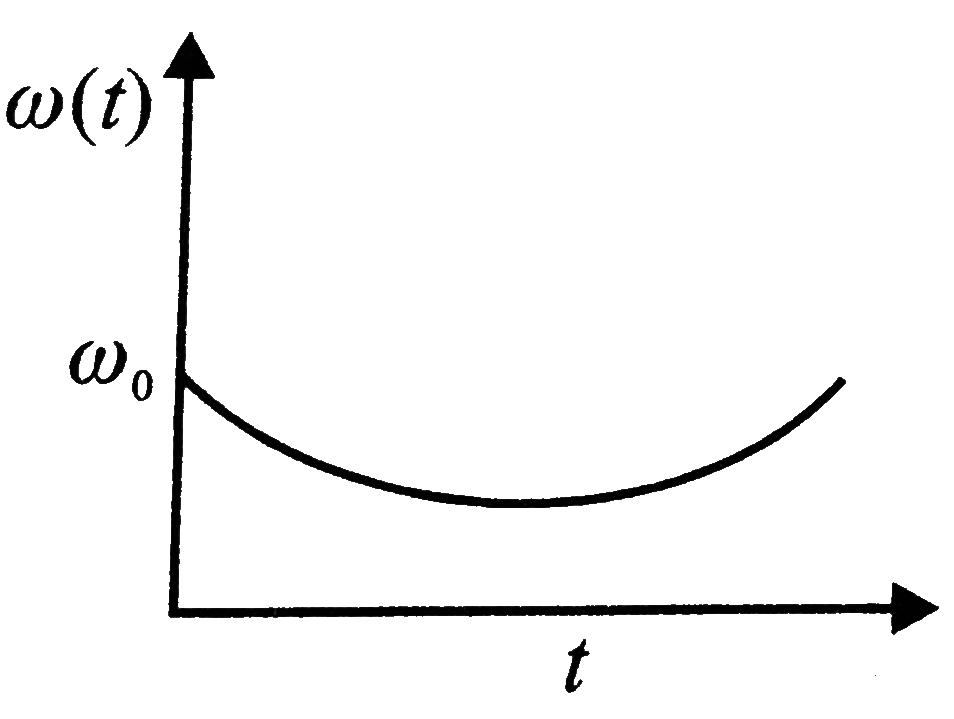
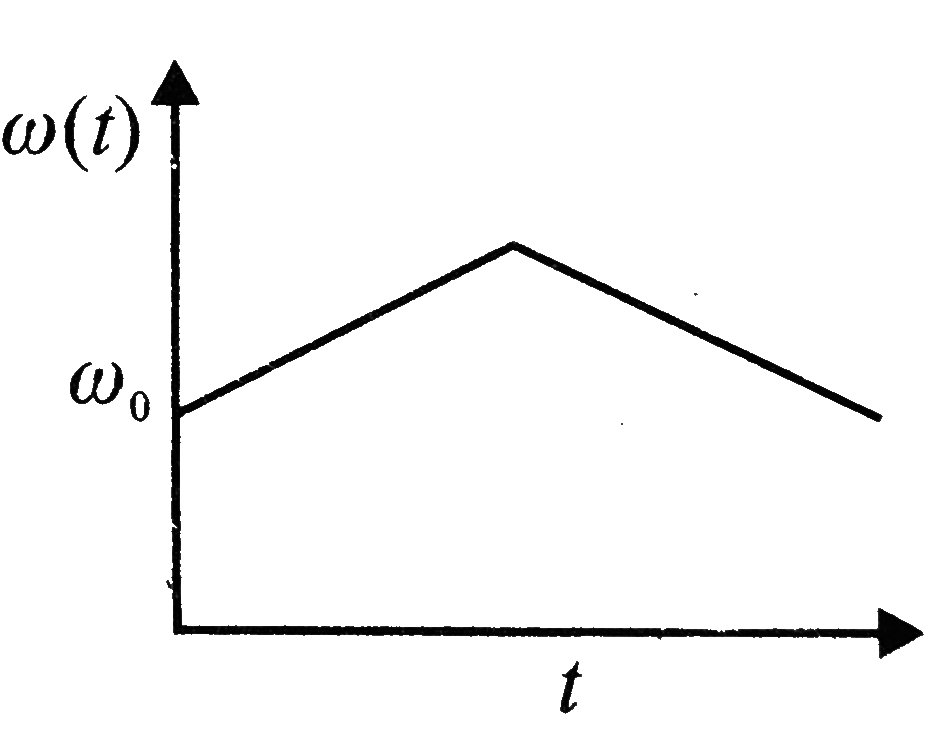
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
RIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise MCQ_TYPE|14 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise AR_TYPE|2 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise True/False|4 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS ENGLISH|Exercise Integer|11 VideosSOUND WAVES AND DOPPLER EFFECT
CENGAGE PHYSICS ENGLISH|Exercise Integer|16 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 2-SCQ_TYPE
- A equilaterial triangle ABC formed from a uniform wire has two small i...
Text Solution
|
- One quarter sector is cut from a uniform circular disc of radius R. Th...
Text Solution
|
- A cylinder rolls up an inclined plane, reaches some height and then ro...
Text Solution
|
- A circular platform is free to rotate in a horizontal plane about a ve...
Text Solution
|
- Consider a body, shown in figure, consisting of two identical balls, e...
Text Solution
|
- A particle undergoes uniform circular motion. About which point on the...
Text Solution
|
- A horizonral circular plate is rotating about a vertical axis passing ...
Text Solution
|
- A disc is rolling (without slipping) on a horizontal surface. C is its...
Text Solution
|
- A block of mass m is at rest under the action of force F against a wal...
Text Solution
|
- From a uniform circular disc of radius R and mass 9M, a small disc of ...
Text Solution
|
- A particle is confined to rotate in a circular path decreasing linear ...
Text Solution
|
- A solid sphere of mass M, radius R and having moment of inertia about ...
Text Solution
|
- A small object of uniform density rolls up a curved surface with an i...
Text Solution
|
- If the resultant of all the external forces acting on a system of part...
Text Solution
|
- A block of base 10cmxx10cm and height 15cm is kept on an inclined plan...
Text Solution
|
- A thin ring of mass 2kg and radius 0.5 m is rolling without on a horiz...
Text Solution
|
- A thin uniform rod, pivoted at O, is rotating in the horizontal plane ...
Text Solution
|
- A small mass m is attached to a massless string whose other end is fix...
Text Solution
|
- Two identical discs of same radius R are rotating about their axes in ...
Text Solution
|
- Two solid cylinders P and Q of same mass and same radius start rolling...
Text Solution
|