A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
RIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise AR_TYPE|2 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise LC_TYPE|8 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise SCQ_TYPE|29 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS ENGLISH|Exercise Integer|11 VideosSOUND WAVES AND DOPPLER EFFECT
CENGAGE PHYSICS ENGLISH|Exercise Integer|16 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 2-MCQ_TYPE
- Two particles A and B intiallly at rest, move towards each other under...
Text Solution
|
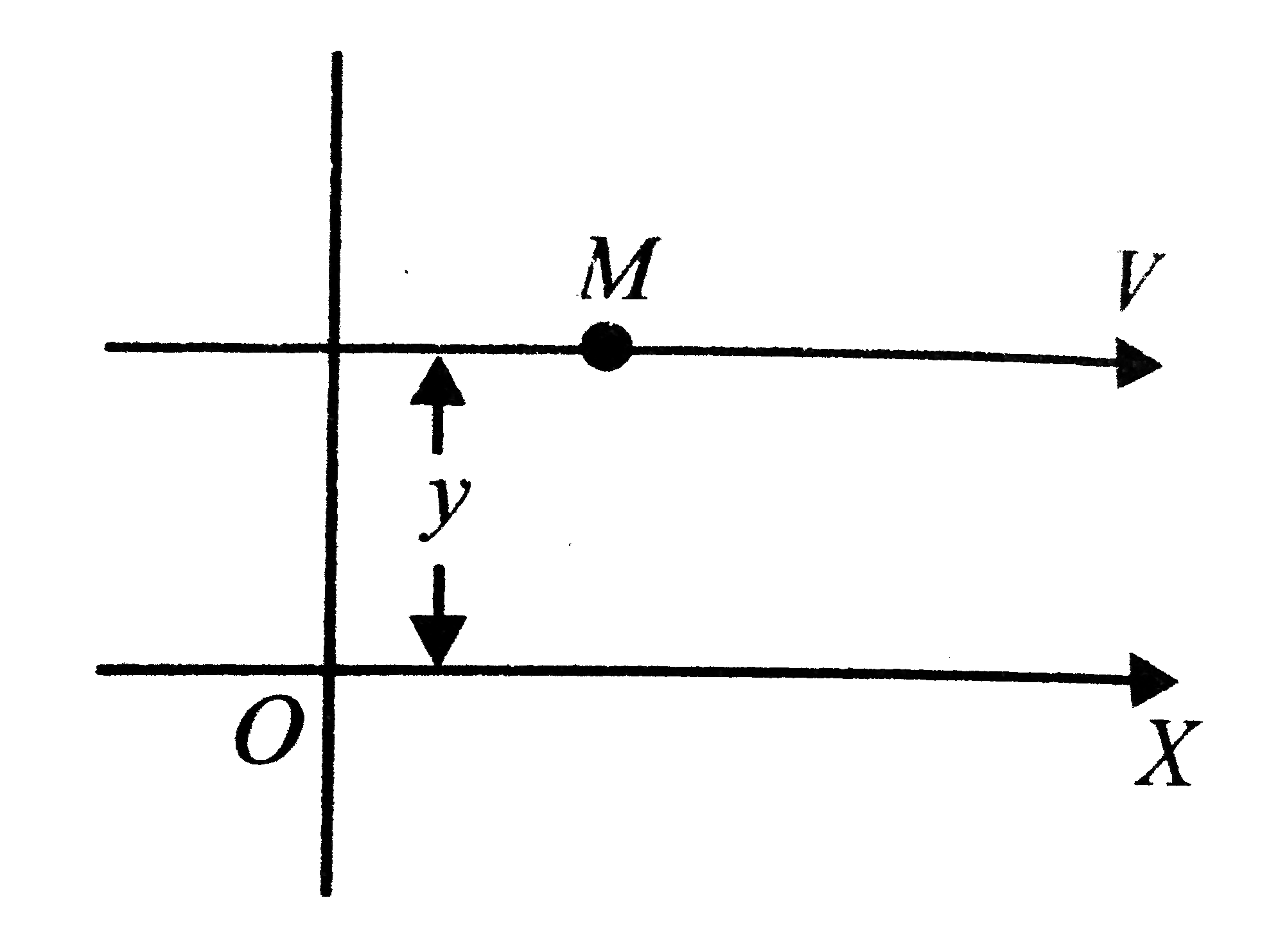
- A mass M moving with a constant velocity parallel to the X-axis. Its a...
Text Solution
|
- When a bicycle is in motion, the force of friction exerted by the grou...
Text Solution
|
- A particle of mass m is projected with a velocity v making an angle of...
Text Solution
|
- The moment of inertia of a thin square plate ABCD of uniform thickness...
Text Solution
|
- A tube of length L is filled completely with an incompressible liquid ...
Text Solution
|
- A car is moving in a circular horizontal track of radius 10 m with a c...
Text Solution
|
- Let I be the moment of inertia of a uniform square plate about an axis...
Text Solution
|
- The torque tau on a body about a given point is found to be equal to A...
Text Solution
|
- A solid cylinder is rolling down a rough inclined plane of inclination...
Text Solution
|
- A ball moves over a fixed track as shown in the figure. From A to B th...
Text Solution
|
- A sphere is rolling without slipping on a fixed horizontal plane surfa...
Text Solution
|
- Two spherical planets P and Q have the same uniform density rho, masse...
Text Solution
|
- The figure shows a system consisting of (i) a ring the outer radius 3R...
Text Solution
|