Text Solution
Verified by Experts
Topper's Solved these Questions
FLUID MECHANICS
CENGAGE PHYSICS ENGLISH|Exercise Exercise 4.2|11 VideosFLUID MECHANICS
CENGAGE PHYSICS ENGLISH|Exercise Exercise 4.3|10 VideosFLUID MECHANICS
CENGAGE PHYSICS ENGLISH|Exercise Solved Examples|7 VideosDIMENSIONS & MEASUREMENT
CENGAGE PHYSICS ENGLISH|Exercise Integer|2 VideosGRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-FLUID MECHANICS-Exercise 4.1
- What is the absolute pressure on a swimmer 10 m below the surface of a...
Text Solution
|
- What will be the length of mercury column in a barometer tube when th...
Text Solution
|
- A U tube contains water and methylated spirit separated by mercury. Th...
Text Solution
|
- A U-tube in which the cross-sectional area of the limb on the left is ...
Text Solution
|
- Figure (b) shows the variation of pressure (p) with depth (h) along a ...
Text Solution
|
- Water stands at a depth of 15 m behind a reservoir dam. A horizontal p...
Text Solution
|
- A glass full of water has a bottom of area 20 cm^(2), top of area 20 c...
Text Solution
|
- An isosceles triangular plates of base 3 m and altitude 3 m is immerse...
Text Solution
|
- Two lock gates of 7.5 m height are provided in a canal of 16 m width m...
Text Solution
|
- Figure shows a semi-cylindrical massless gate pivoted at the point O h...
Text Solution
|
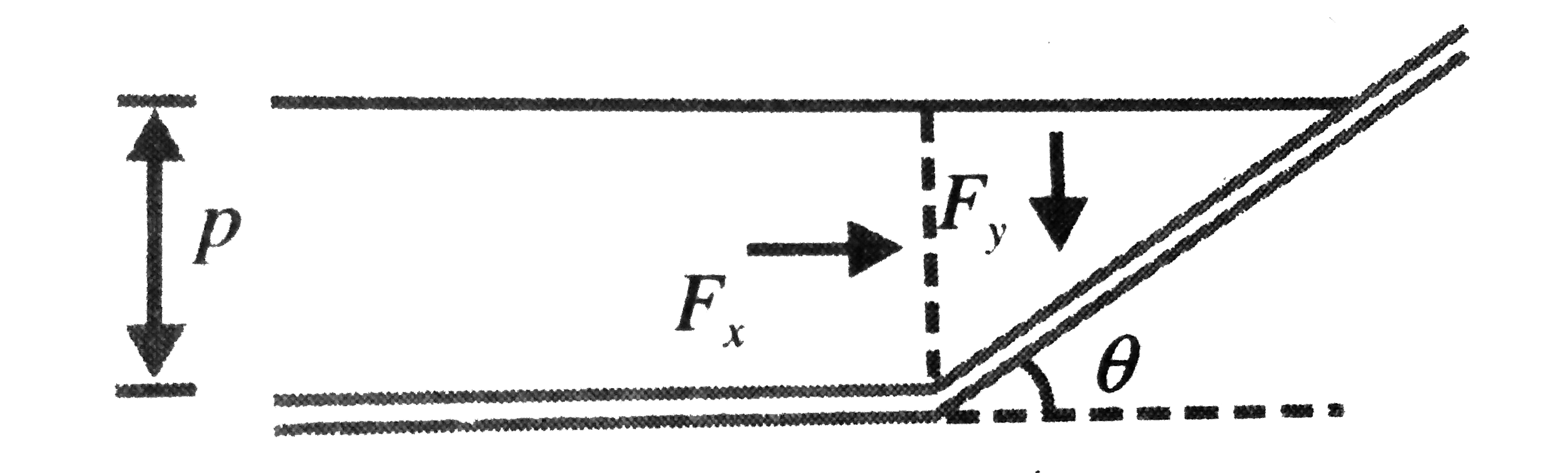
- Consider a container having an inclined wall, inclined an angle theta ...
Text Solution
|