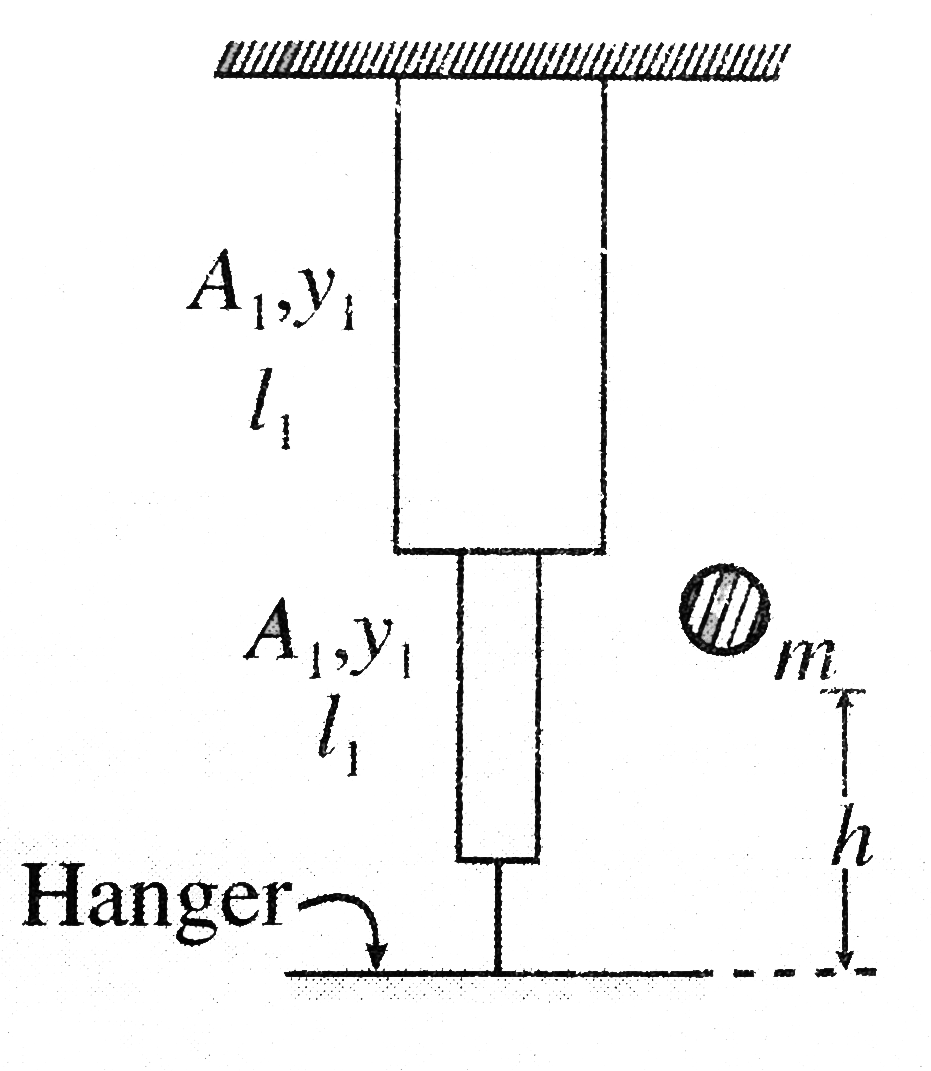Text Solution
Verified by Experts
Topper's Solved these Questions
PROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS ENGLISH|Exercise Exercise 5.2|6 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS ENGLISH|Exercise Exercise 5.3|9 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS ENGLISH|Exercise Solved Examples|11 VideosNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS ENGLISH|Exercise Integer type|1 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS ENGLISH|Exercise Integer|11 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-PROPERTIES OF SOLIDS AND FLUIDS-Exercise 5.1
- Stress and pressure are both forces per unit area. T in what respect d...
Text Solution
|
- The stress and strain graphs for two materials, A and B are shown here...
Text Solution
|
- State whether the following statements are true or false with reasons....
Text Solution
|
- A horizontal force of magnitude Facts at the end P of a uniform rigid ...
Text Solution
|
- A rubber ball of bulk modulus B is taken to a depth h of a liquid of d...
Text Solution
|
- Find out longitudinal stress and tangential stress on a fixed block.
Text Solution
|
- Find out bulk stress on the spherical object of radius 10//pi cm if ar...
Text Solution
|
- Three rods of uniform area of cross section A =10^(-7)m^(2) are arrang...
Text Solution
|
- Find the depth of lake at which density of water is 1% greater than th...
Text Solution
|
- A rubber cube of side 5 cm has one side fixed while a tangential force...
Text Solution
|
- A mass 'm' is attached with rods as shown in Fig. This mass is slightl...
Text Solution
|
- A ball of mass 'm' drops from a height which sticks to a massless hang...
Text Solution
|