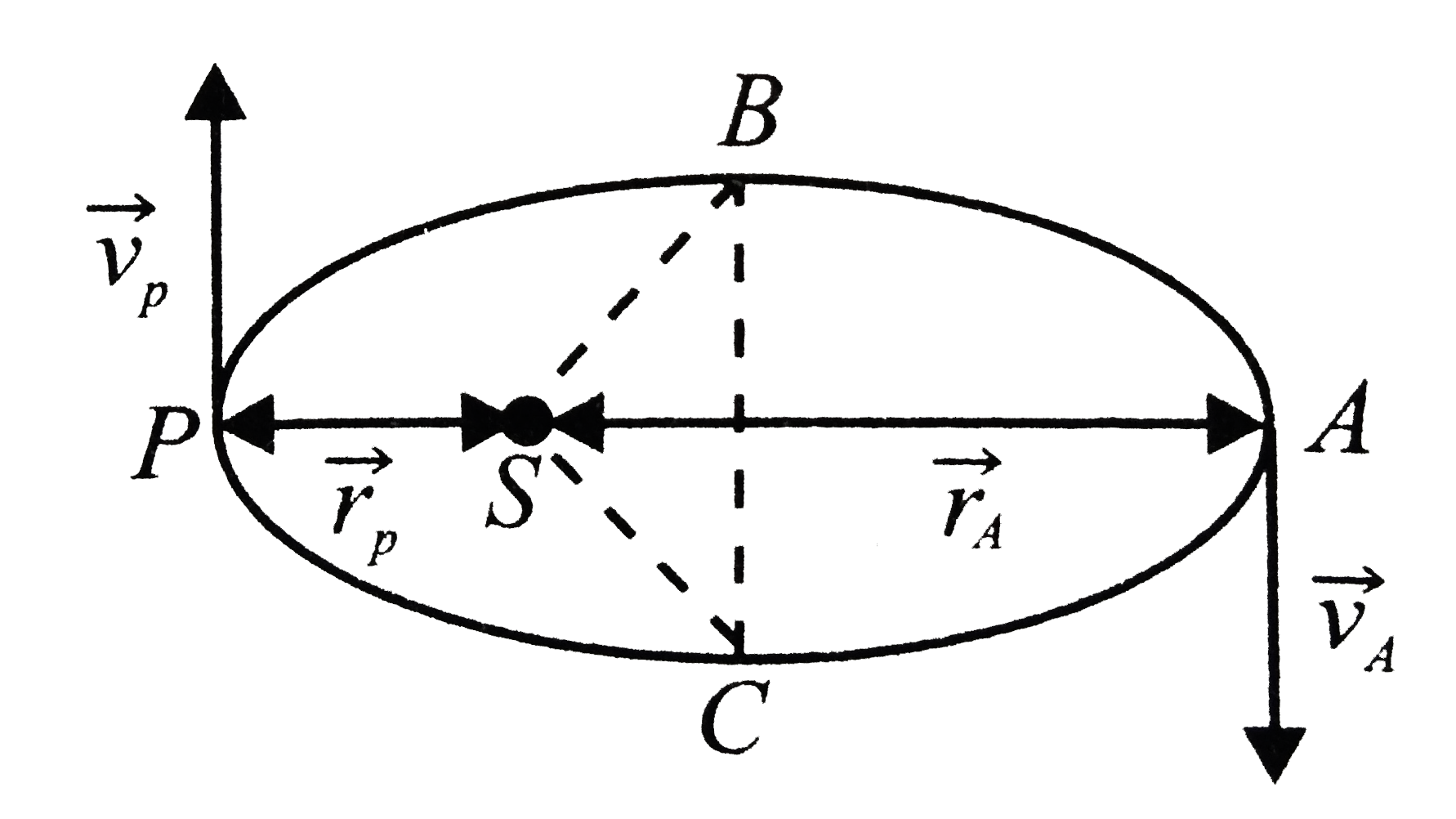
Let the speed of the planet at the perhelion Pin Fig. 8.1 (a) be `v_(p)` and the sun-planat distance SP be `r_(p)`. Relate `(r_(p')v_(p))` to the corresponding quantities at the aphelion `(r_(A).v_(A))` will the planat take equal times to traverse BAC and CPB?
Let the speed of the planet at the perhelion Pin Fig. 8.1 (a) be `v_(p)` and the sun-planat distance SP be `r_(p)`. Relate `(r_(p')v_(p))` to the corresponding quantities at the aphelion `(r_(A).v_(A))` will the planat take equal times to traverse BAC and CPB?
Text Solution
Verified by Experts
Referring fig we note that `vecr_(P)` and `vecv_(P)` are perpendicular to each other. Similarly `vecr_(A)` and `vecv_(A)` are perpendicular to each. Using the law of conservation of angular momentum,
Angular momentum of the plane at `P=` Angular momentum of the planet at `A`
`impliesm_(P)v_(P)r_(P)=m_(A)v_(A)r_(A)`
or `(v_(P))/(v_(A))=(r_(A))/(r_(P))`
Since `r_(A)gtr_(P), v_(P)gtv_(A)`
Her area `SBAC` is greater than area `SCPB`. As the areal velocity of a planet is contant aroung the Sun i.e. equal areas are swept in equal times. Hence the planet will take longer time to reverse `BAC` than `CPB`.
Angular momentum of the plane at `P=` Angular momentum of the planet at `A`
`impliesm_(P)v_(P)r_(P)=m_(A)v_(A)r_(A)`
or `(v_(P))/(v_(A))=(r_(A))/(r_(P))`
Since `r_(A)gtr_(P), v_(P)gtv_(A)`
Her area `SBAC` is greater than area `SCPB`. As the areal velocity of a planet is contant aroung the Sun i.e. equal areas are swept in equal times. Hence the planet will take longer time to reverse `BAC` than `CPB`.

Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
Let the speed of the planet at the perihelion P in figure be v_(P) and the Sun planet distance SP be r_(P) . Relater r_(P), v_(P) to the corresponding quantities at the aphelion (r_(A),v_(A)) . Will the planet take equal times to transverse BAC and CPB ?
Let V and I respresent, respectively, the readings of the voltmeter and ammetre shows in Fig. 6.34 , and let R_(V) and R_(V) be their equivalent resistances. Because of the resistances of the meters, the resistnce R is not simply equal to V//I . (a) When the circuit is connected as shows in Fig. 6.34 (a), shows that R = (V)/(I) - R_(A) Explain why the true resistance R is always less than V//I . (b) When the connections are as shows in Fig. 6.34 (b) Show that R = (V)/(I - (V//R_(V))) Explain why the true resistance R is always greater than V//I . (c ) Show that the power delivered to the resistor in part (i) is IV - I^(2) R_(A) and that in part (ii) is IV - (V^(2)//R_(V))
A planet orbits the sun in an elliptical path as shown in the figure. Let v_(p) " and " v_(A) be spped of the planet when at perohelion and aphelion respectively. Which of the following relations is correct ?
A planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
A plenet moving along an elliptical orbit is closest to the sun at a distance r_(1) and farthest away at a distance of r_(2) . If v_(1) and v_(2) are the linear velocities at these points respectively, then the ratio (v_(1))/(v_(2)) is
A satellite of mass m orbits the earth in an elliptical orbit having aphelion distance r_(a) and perihelion distance r_(p) . The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are (r_(a) + r_(p))/(2) and sqrt(r_(p)r_(a)) respectively. The angular momentum of the satellite is: (A) (2m pi (r_(B)+r_(p)) sqrt(r_(a) r_(p)))/T (B) (m pi (r_(a)+r_(p)) sqrt(r_(a) r_(p)))/(2T) (C) (m pi (r_(a)+r_(p)) sqrt(r_(a)r_(p)))/(4T) (D) (mpi (r_(a)+r_(p)) sqrt(r_(a)r_(p)))/T
A planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to r_(a) and r_(p) respectively. Find the angular momentum of this planet relative to the sun.
The pressure p and the volume v of a gas are connected by the relation p v^(1. 4)=con s tdot Find the percentage error in p corresponding to a decrease of % in vdot
A planet is revolving around the sun. its distance from the sun at apogee is r_(A) and that at perigee is r_(p) . The masses of planet and sun are 'm' and M respectively, V_(A) is the velocity of planet at apogee and V_(P) is at perigee respectively and T is the time period of revolution of planet around the sun, then identify the wrong answer.
A planet is revolving round the sun is elliptical orbit. Velocity at perigee position ( nearest) is v_(1) and at apogee position ( farthest) is v_(2) . Both these velocities are perpendicular to the line joining centre of sun and planet. r_(1) is the minimum distance and r_(2) the maximum distance. At apogee position suppose speed of planet is slightly decreased from v_(2) , then what will happen to minimum distance r_(1) and maximum distance r_(2) in the subsequent motion.