Home
Class 11
PHYSICS
Three equal masses 2m each are placed at...

Three equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m

Text Solution

Verified by Experts

a. From figure the gravitational force on mass `2m` at `G` due to mas at `A` is
`F_(1)=G(mxx2m)/(1^(2))=2Gm^(2)` along `GA`
Gravitational force of mass `2m` at `G` due to mass at `B` is
`F_(2)=G(mxx2m)/(1^(2))=2Gm^(2)` along `BG`

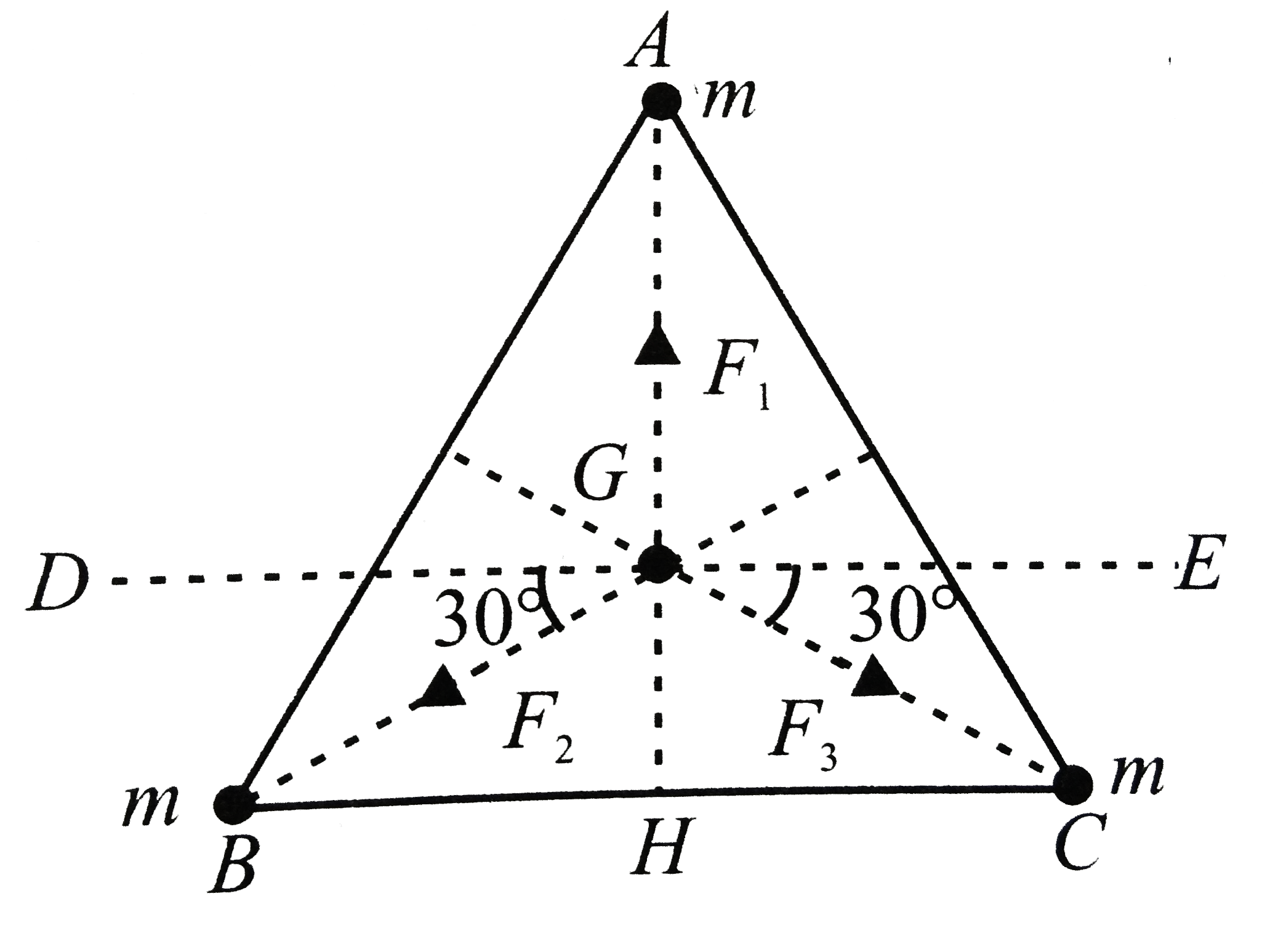
Gravitational force on mass `2m` at `G` due to mass at `C` is
`F_(3) G(mxx2m)/(1^(2))=2Gm^(2)` along `GC`
Draw `DE` parallel to `BC` passing through point `G`. Then
`/_EGC=30^@=/_DGB`.
Resolving `vecF_(2)` and `vecF_(3)` into two rectangular components we have
`F_(2)cos30^@` along `GD` and `F_(2)sin30^@` along `GH`
`F_(3)cos30^@` along `GE` and `F_(3)` and `30^@` along `GH`
Here `F_2cos30^@` and `F_3 sin 30^@` are equal in magnitude and acting in opposite directions, and cancel in magnitude and acting opposite directions, and cancel out each other.
The resultant force on mass `2m` at `G` is
`F_(1)-(F_(2)sin30^@=F_(3)sin30^@)`
`=2Gm^(2)-(2Gm^(2)xx1/2+2Gm^(2)xx1/2)`
`=0`
b. When mass at `A` is `2m`, then gravitational force on mass `2m` at `G` due to mass `2m` at `A` is
`F_(1)^(')=G(2mmxx2mm)/(1^(2))=4Gm^(2)` along `GA`
The resultant force on mass `2m` at `G` due to masses at At, `B` and `C` is
`F_(1)^(')=(F_(2)sin30^@+F_(3)sin30^@)`
`=4Gm^(2)-(2Gmxx1/2+2Gm^(2)xx1/2)`
`=2Gm^(2)` along `GA`
Promotional Banner

Topper's Solved these Questions

  • GRAVITATION

    CENGAGE PHYSICS ENGLISH|Exercise Exercise 6.1|13 Videos

  • GRAVITATION

    CENGAGE PHYSICS ENGLISH|Exercise Exercise 6.2|15 Videos

  • FLUID MECHANICS

    CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 Videos

  • KINEMATICS-1

    CENGAGE PHYSICS ENGLISH|Exercise Integer|9 Videos

Similar Questions

Explore conceptually related problems

Three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC . a. What is the force acting on a mass 2m placed at the centroid G of the triangle? b. What is the force if the mass at the vertex A is doubled? Take AG=BG=CG=1m

Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is

Three equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?

Three masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?

Three equal masses each of mass 'm' are placed at the three-corner of an equilateral triangle of side 'a' If a fourth particle of equal mass is placed at the centre of triangle, then net force acting on it, is equal to

Consider three charges q_(1),q_(2) and q_(3) each equal to q , at the vertices of an equilateral triangle of side l. What is the force on a charge Q placed at the centroid of the triangle?

Consider three charges q_(1),q_(2) and q_(3) each equal to q , at the vertices of an equilateral triangle of side l. What is the force on a charge Q placed at the centroid of the triangle?

Three equal masses of 2kg each are placed at the vertices of an equilateral triangle and a mass of 4 kg is placed at the centroid of the triangle which is at a distance of sqrt(2) m from each of the vertices of the triangle. The force, (in newton) acting on the mass of 4 kg is

Three mass points each of mass m are placed at the vertices of an equilateral triangle of side 1. What is the gravitational field and potential due to the three masses at the centroid of the triangle ?

Three equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)