Three particles each of mass m, are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?
.

Explanation

Refer to figure, force of attraction on body at `C` due to body at `A` is
`F_(1)=(Gmm)/(r^(2))=(Gm^(2))/(r^(2))` along `CA`
Force of attraction on body at `C` due to body at `B` is
`F_(2)=(Gmm)/(r^(2))=(Gm^(2))/(r^(2))` along `CB`.

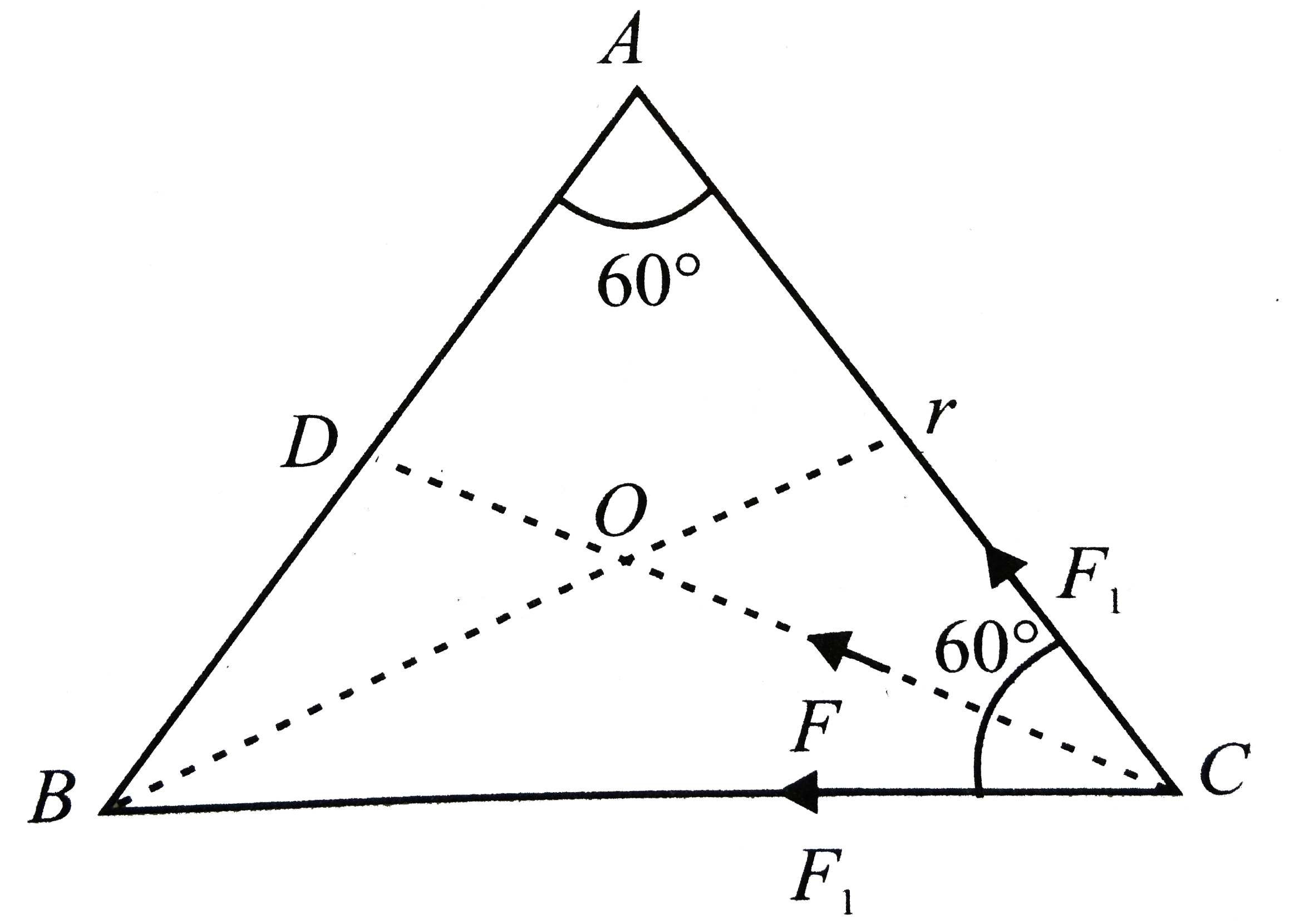
These force `vecF_(1)` and `vecF_(2)` are inclined at an angle `60^@`. the resultant force on the body at `C` is
`F=sqrt(F_(1)^(2)+F_(2)^(2)+2F_(1)F_(2)cos60^@)`
`=sqrt(F_(1)^(2)+F_(2)^(2)+2F_(1)F_(2)(1/2))`
`sqrt(3)F_(1)=sqrt(3)(Gm^(2))/(r^(2))` acting along CD
`:'F_(1)=F_(2)=[(Gm^(2))/(r^(2))]`
Here `OC=2/3 C=2/3ACsin60^@`
`=2/3rxx(sqrt(3))/2=r/(sqrt(3))`
When each body is describing a circular orbit with cenre of orbit at `O`, the force `F` provides the required centripetal force. The radius of the circular orbit is `OC=r//sqrt(3)`. If `v` is the speed of the body in circular orbit, then
`(Mv^(2))/(r//sqrt(3))=(sqrt(3)Gm^(2))/(r^(2))` or `v=sqrt((Gm)/r)`