Figure shows a spherical cavity inside a lead sphere. The surface of the cavity passes through the centre of the sphere and touches the right side of the sphere. The mass of the sphere before hollowing was `M`. With what gravitational force does the hollowed out lead sphere attract a particle of mass `m` that lies at a distance `d` from the centre of the lead sphere on the straight line connecting the centres of the spheres and of the cavity.

Explanation

Let `O` be the centre of the solid sphere and `O'` that of the hollow. For an external point the sphere behaves as if is entire mass is concentrated at its centre. Therefore, the gravitatioinal foorce on a mass `m` at `P` due to the original sphere (of mass `M`) is

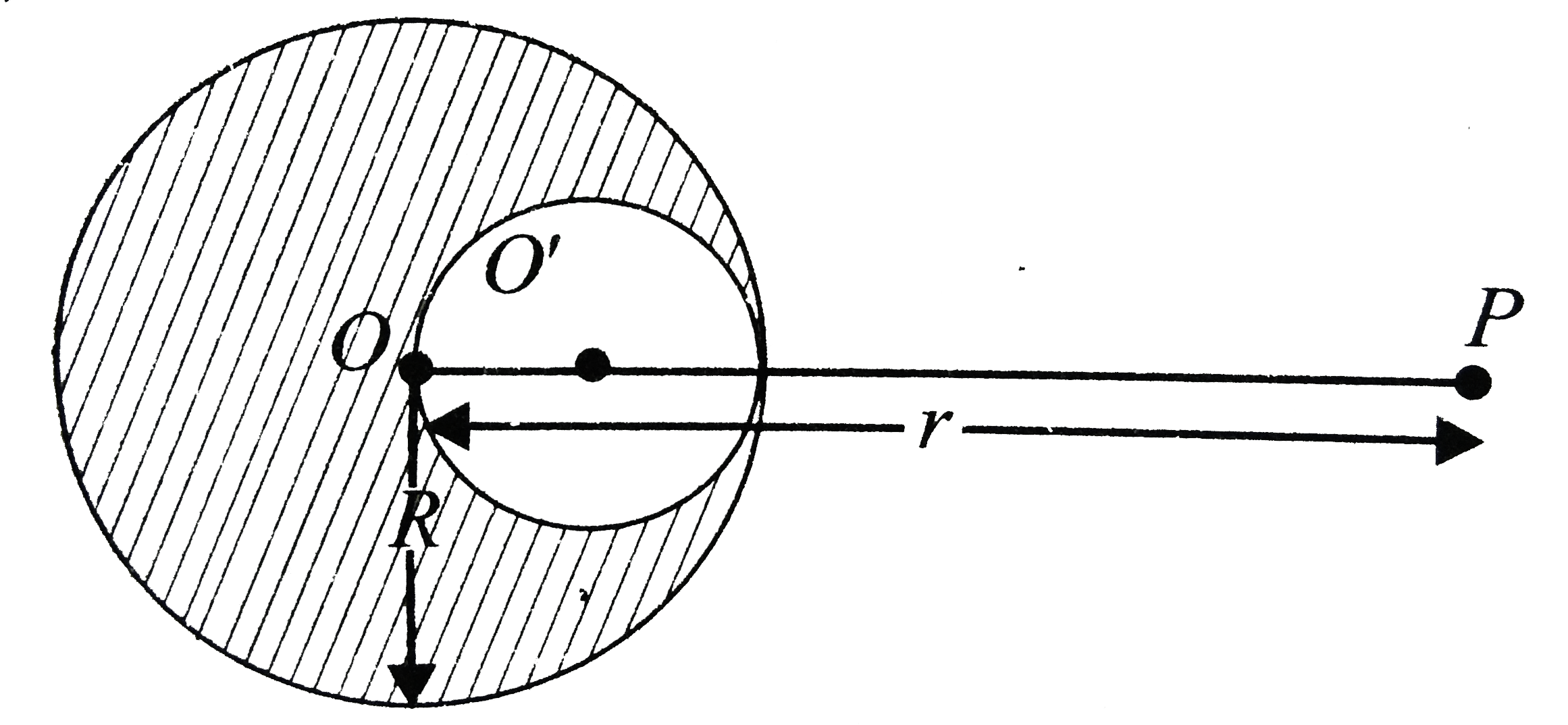
`F=G(Mm)/(r^(2)),` along `PO`
The diameter of the smaller sphere (which would be cut of) is `R`, so that its radius `OO'` is `R//2`. The force on `m` at `P` due to this sphere of mass `M` (say) would be
`F'=G(M'm)/((r-R/2)^(2))` along `PO'` (`:'` distance `PO'=r-R//2)`
As the radius of this sphere is half of that of the original sphere, we have
`M'=m/8`
Therefoe `F'=G(Mm)/(8(r-R//2)^(2))` along `PO'`
As both `F` and `F'` point along the same direction, the force due to the hollowed sphere is
`F-F^(')=(GMm)/(r^(2))-(GMm)/(8r^(2)(1-R/(2r)^(2))`
`=(GMm)/(r^(2)) {1- 1/(8(1-R/(2R)^(2)))}`