Home
Class 11
PHYSICS
Distance between the centres of two star...

Distance between the centres of two stars is `10a`. The masses of these stars are `M` and `16 M` and their radit `a` and `2a` respectively. A body of mass `m` is fired straight from the surface of the larger star towards the smaller star. What should be its minimum inital speed to each the surface of the smaller star? Obtain the expression in terms of `G`, `M` and `a`.

Text Solution

Verified by Experts

Let `P` be the point on the joining the centres of the two planets such that the net field at that point is zero.

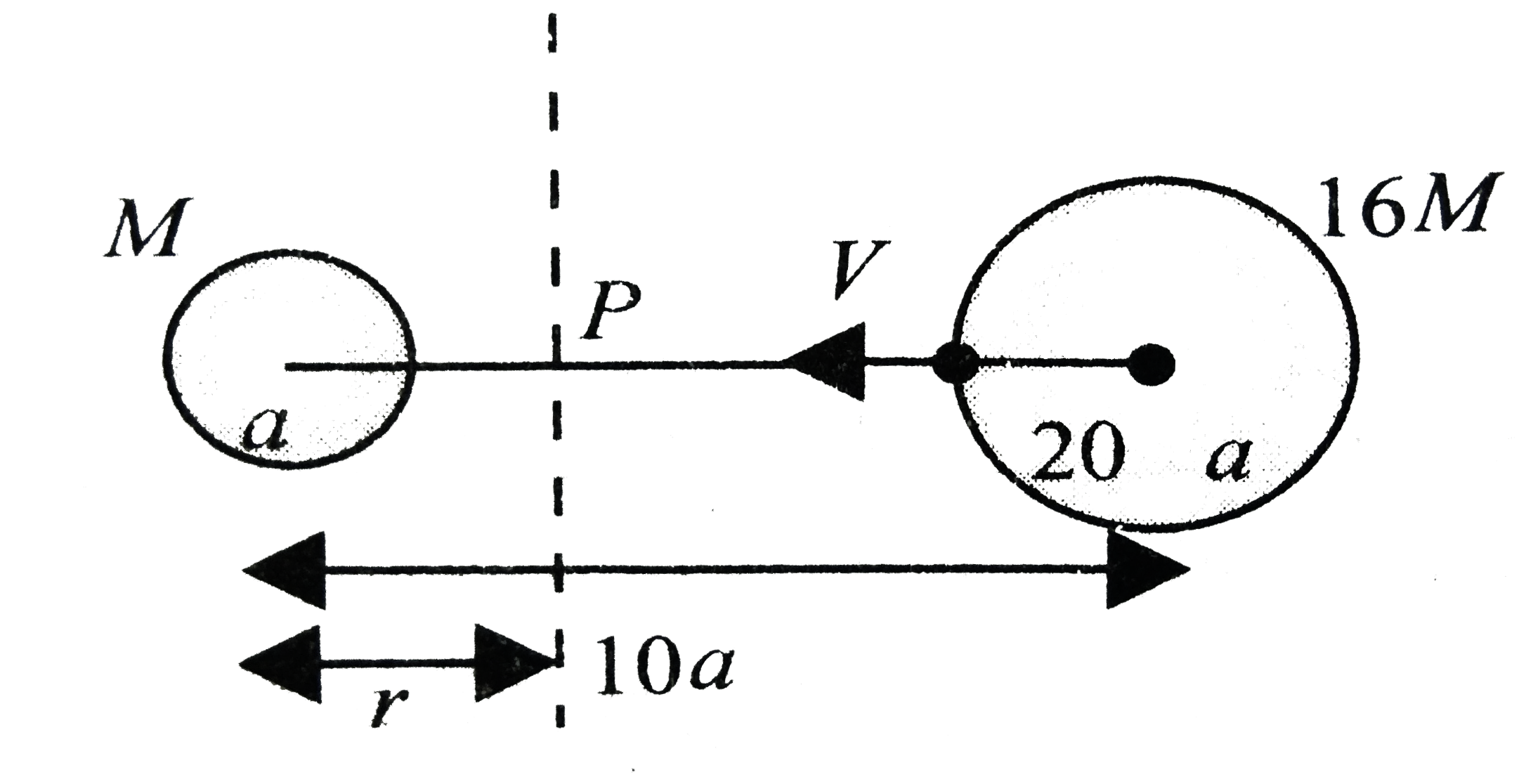
Then `(GM)/(r^(2))-(G16M)/((10a-r)^(2))=0`
`implies(10a-r)^(2)=16r^(2)`
`implies 10a-r=4r`
`impliesr=2a`
Potential at point `P`
`v_(P)=(-GM)/r=(G16M)/((10a-r))=(-GM)/(2a)-(2GM)/a`
`(-5GM)/(2a)`
Now if the particle projected from the larger planet has enough energy to cross this point, it will reach the smaller planet.
For this, the `KE` imparted to the body must be just enough to raise its total mechanical enrgy to a value which is equal to `PE` at point `P`, i.e.
`1/2mv^(2)-(G(16M)m)/(2a)-(GMm)/(8a)=mv_(P)`
or `(v^(2))/2-(8GM)/a-(GM)/(8a)=(5GMm)/(2a)`
or `v^(2)=(45GM)/(4a)`
or `v_(min)=3/2sqrt((5GM)/a)`
Promotional Banner

Topper's Solved these Questions

  • GRAVITATION

    CENGAGE PHYSICS ENGLISH|Exercise Exercise 6.1|13 Videos

  • GRAVITATION

    CENGAGE PHYSICS ENGLISH|Exercise Exercise 6.2|15 Videos

  • FLUID MECHANICS

    CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 Videos

  • KINEMATICS-1

    CENGAGE PHYSICS ENGLISH|Exercise Integer|9 Videos

Similar Questions

Explore conceptually related problems

Distance between the centres of two stars is 10a . The masses of these stars are M and 16 M and their radii a and 2a respectively. A body of mass m is fired straight from the surface of the larger star towards the surface of the smaller star. What should be its minimum initial speed to reach the surface of the smaller star? Obtain the expression in terms of G , M and a.

Distance between the centres of two stars is 10a . The masses of these stars are M and 16 M and their radii a and 2a respectively. A body of mass m is fired straight from the surface of the larger star towards the surface of the smaller star. What should be its minimum initial speed to reach the surface of the smaller star? Obtain the expression in terms of G , M and a .

Distance between the centres of two rings is a. The masses of these rings are M and 4M . A body of mass m is fired straight from the centre of the heavier ring. What should be its minimum initial speed to cross of lighter ring ? The radius of the both ring is R . (Assume a gt gt R ).

Two planets have masses M and 16 M and their radii are a and 2a, respectively. The separation between the centres of the planets is 10a. A body of mass m is fired trom the surface of the larger planet towards the samller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :

The distance of centre of mass from point O of two square plates system, as shown,( if masses of plates are 2m and m and their edges are 'a' and '2a' respectively) is

A fixed spherical shell of inner radius R and outer radius 2R has mass M, A particle of mass m is held at rest at a distance 2R from the surface of the body. If the particle is released from that point, with what speed will it hit surface of the spherical body ?

Two homogeneous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in touch . The distance of the centre of mass from the first sphere is

Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a . Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.

A body of mass 2 kg is dropped from rest from a height 20 m from the surface of Earth. The body hits the ground with velocity 10 m/s, then work done: (g=10m//s^(2))

What impulse need to be given to a body of mass m , released from the surface of earth along a straight tunnel passing through centre of earth, at the centre of earth, to bring it to rest. (Mass of earth M, radius of earth R)