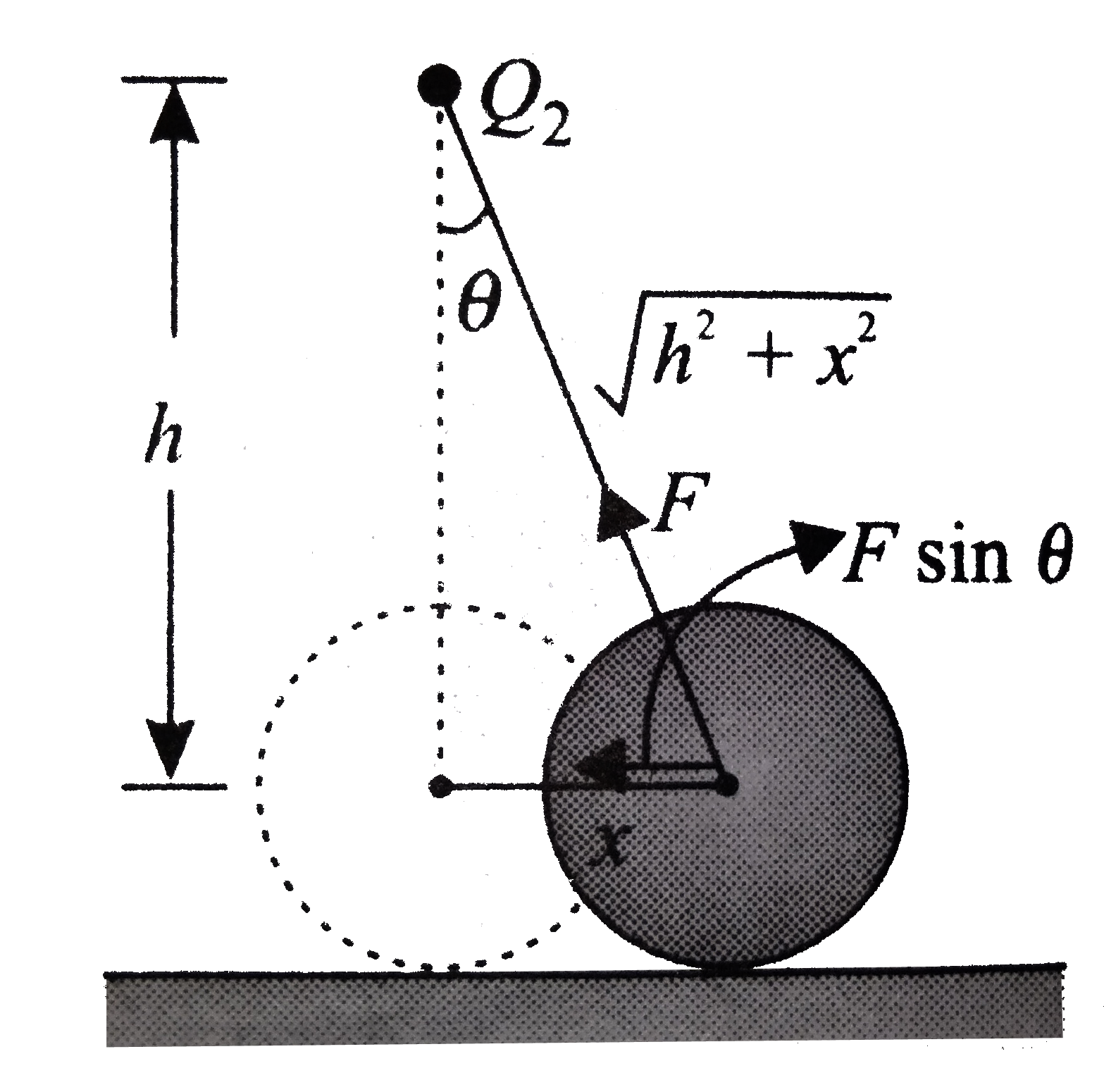Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
COULOMB LAW AND ELECTRIC FIELD
CENGAGE PHYSICS ENGLISH|Exercise Single Correct|47 VideosCOULOMB LAW AND ELECTRIC FIELD
CENGAGE PHYSICS ENGLISH|Exercise Multiple Correct|8 VideosCOULOMB LAW AND ELECTRIC FIELD
CENGAGE PHYSICS ENGLISH|Exercise Subjective Type|15 VideosCENGAGE PHYSICS DPP
CENGAGE PHYSICS ENGLISH|Exercise subjective type|51 VideosELECTRIC CURRENT & CIRCUITS
CENGAGE PHYSICS ENGLISH|Exercise Kirchhoff s law and simple circuits|15 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-COULOMB LAW AND ELECTRIC FIELD-Subjective
- Point chages q and -q are located at the verticles of a squre with dia...
Text Solution
|
- Two mutually perpendicular long straight conductors carrying uniformly...
Text Solution
|
- A ring of radius 0.1m is made out of thin metallic wire of area of cro...
Text Solution
|
- A charged cork ball of mass m is suspended on a light sting in the pre...
Text Solution
|
- A ring of radius R has charge -Q distributed uniformly over it. Calcul...
Text Solution
|
- Two identical small equally charged conducting balls are suspended fro...
Text Solution
|
- Two point like charges Q(1) and Q(2) are positioned at point 1 and 2. ...
Text Solution
|
- Two semicircle wires ABC, and ADC, each of radius R are lying on xy an...
Text Solution
|
- An infinte wire having linear charge density lambda is arranged as sho...
Text Solution
|
- Two similar balls, each of mass m and charge q, are hung from a common...
Text Solution
|
- Three equal negative charges, -q(1) each form the vertices of and equi...
Text Solution
|
- A ball of radius R carries a positive charges whose volume density at ...
Text Solution
|
- A uniform nonconducting rod of mass ma and length l, with charge densi...
Text Solution
|
- Electrically charged drops of nercury fall from an altitude h into a s...
Text Solution
|
- A thin rigid insulated rod of mass m and length l carrying a charge Q ...
Text Solution
|
- Two particles of chargaes and masses (+q(1),m(1)) and (+q(2),m(2)) are...
Text Solution
|
- A small beads of mass ma having charge -q is constrained to move along...
Text Solution
|
- A charged particle q of mass m is in wquilibrium at a height h from a ...
Text Solution
|
- A point charge Q(1)=-125mu C is fixed at the center of an insulated di...
Text Solution
|
- Two small balls having the same mass and charge and located on the sam...
Text Solution
|