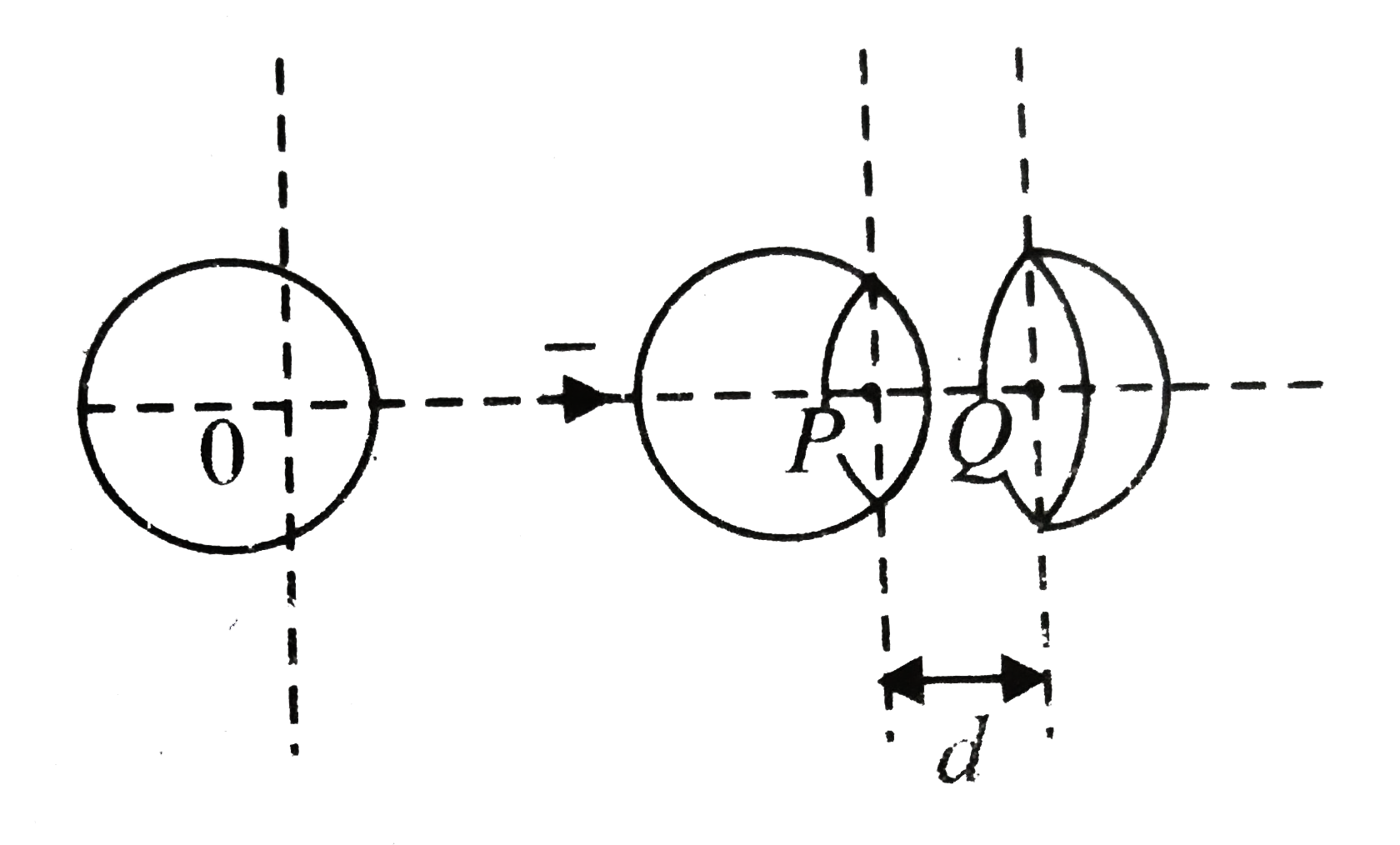A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An insulating spherical shell of uniform surface charge density is cut...
Text Solution
|
- An insulating spherical shell of uniform surface charge density is cut...
Text Solution
|
- Shown in the figure a spherical shell with an inner radius 'a' and an ...
Text Solution
|
- Two identical bar magnets are fixed with their centres at a distance d...
Text Solution
|
- The electric field inside a spherical shell of uniform surface charge ...
Text Solution
|
- The electric field inside a spherical shell of uniform surface charge ...
Text Solution
|
- दो एकसमान दण्ड चुम्बक जिनके केन्द्रों के बीच की दूरी d है। एक आवेशQ दो...
Text Solution
|
- Three large plates having uniform surface charge densities are shown i...
Text Solution
|
- A point charge q is placed at a distance d from centre of a uniformly...
Text Solution
|