Half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
Half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
A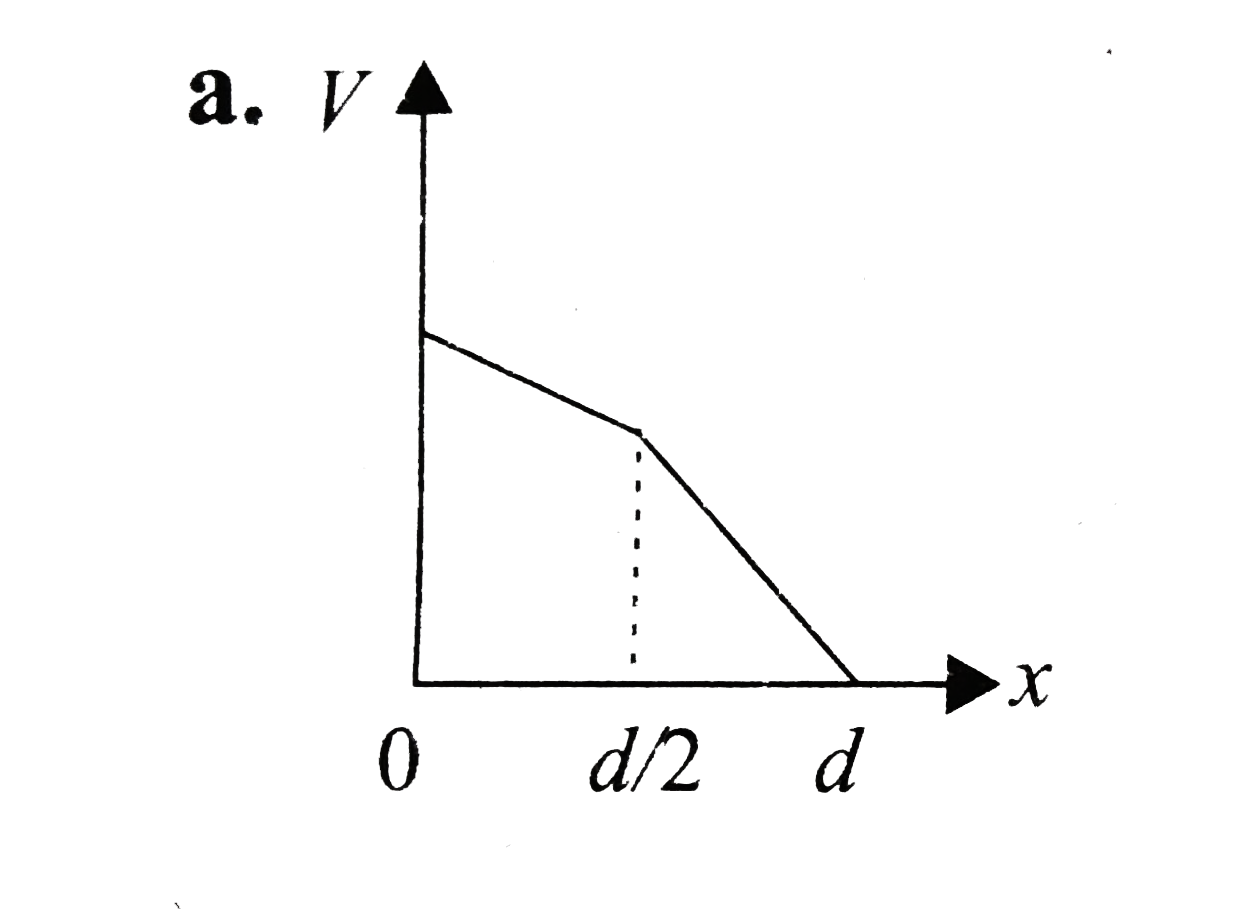

B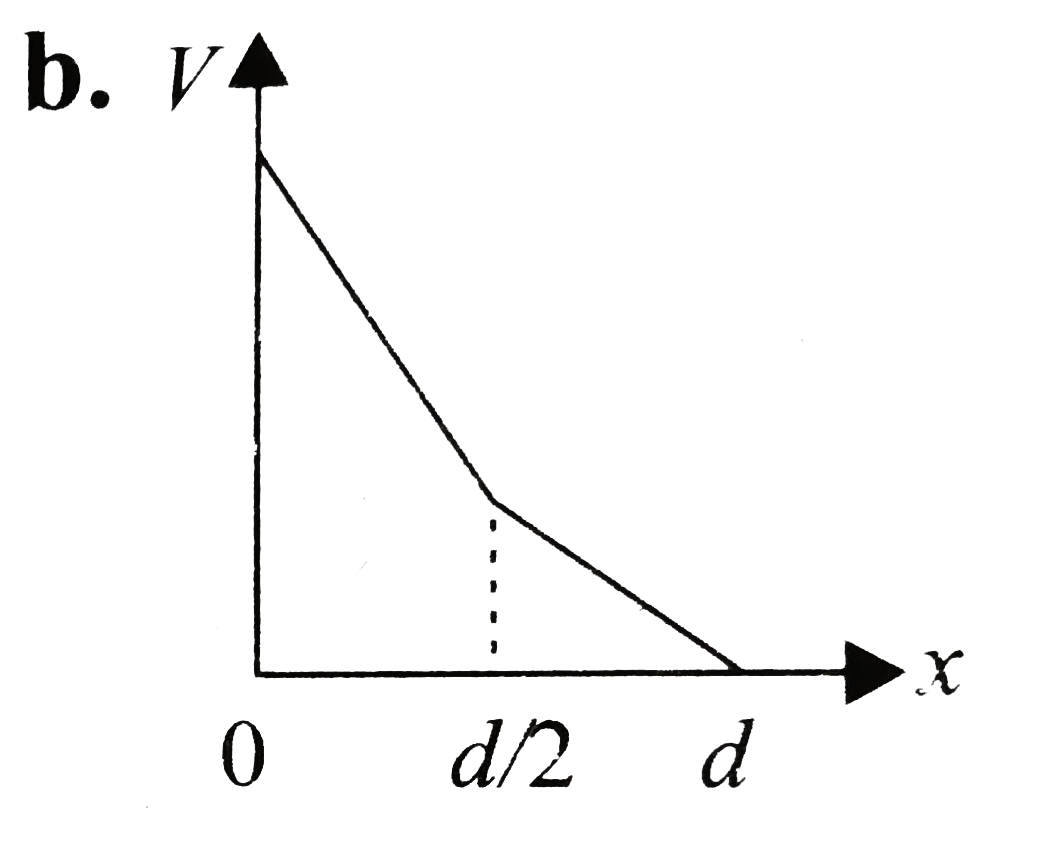

C

D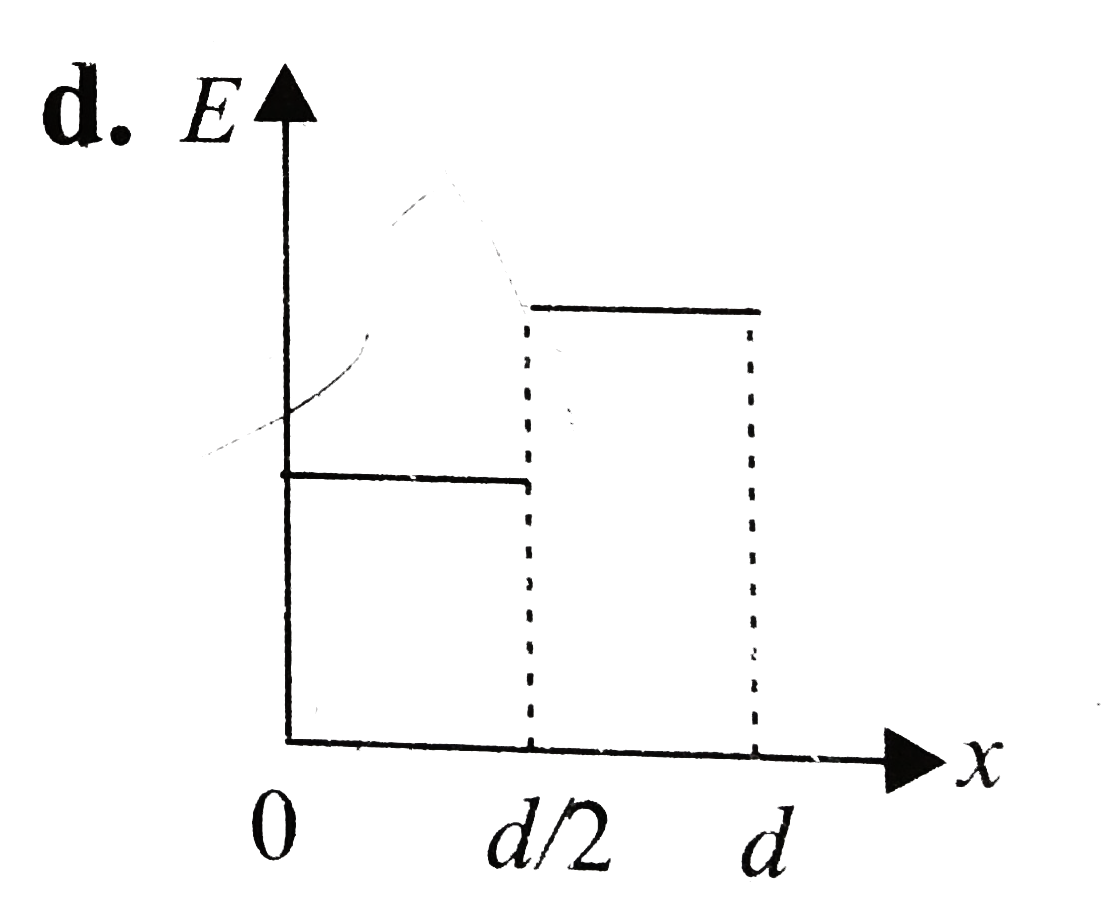

Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem of a parallel plate capacitor with half of the space filled with a dielectric material of constant \( K \), we will analyze the electric field and potential difference across the capacitor.
### Step-by-Step Solution:
1. **Understanding the Configuration**:
- A parallel plate capacitor consists of two plates separated by a distance \( d \).
- In this case, half of the space (i.e., \( d/2 \)) is filled with a dielectric material of constant \( K \), and the other half is air (or vacuum).
2. **Electric Field in Different Regions**:
- Let \( E \) be the electric field in the air gap (the region without the dielectric).
- In the dielectric region, the electric field \( E' \) can be expressed as:
\[
E' = \frac{E}{K}
\]
- This is because the presence of the dielectric reduces the electric field strength by a factor of \( K \).
3. **Potential Difference Calculation**:
- The potential difference \( V \) across the capacitor can be calculated by integrating the electric field over the distance.
- For the air gap (first half):
\[
V_{\text{air}} = E \cdot \frac{d}{2}
\]
- For the dielectric (second half):
\[
V_{\text{dielectric}} = E' \cdot \frac{d}{2} = \frac{E}{K} \cdot \frac{d}{2}
\]
- Therefore, the total potential difference \( V \) across the capacitor is:
\[
V = V_{\text{air}} + V_{\text{dielectric}} = E \cdot \frac{d}{2} + \frac{E}{K} \cdot \frac{d}{2}
\]
- Simplifying this gives:
\[
V = \frac{dE}{2} \left(1 + \frac{1}{K}\right)
\]
4. **Graphical Representation**:
- For the electric field \( E \) versus position \( x \):
- In the air gap, the electric field \( E \) is constant.
- In the dielectric, the electric field \( E' \) is constant but lower than \( E \).
- Therefore, the graph of \( E \) versus \( x \) will show a step down at the boundary of the dielectric.
- For the potential difference \( V \) versus position \( x \):
- The slope of \( V \) in the dielectric region will be less steep than in the air gap due to the reduced electric field.
- Hence, the graph of \( V \) versus \( x \) will show a steeper slope in the air gap and a gentler slope in the dielectric.
5. **Conclusion**:
- The possible plots for the electric field and potential difference are:
- Electric field \( E \) versus position \( x \): a step function with a drop at the dielectric boundary.
- Potential difference \( V \) versus position \( x \): a linear function with a steeper slope in the air gap and a gentler slope in the dielectric.
### Final Answer:
The possible plots are:
- Electric field \( E \) versus position \( x \): Option D (step function).
- Potential difference \( V \) versus position \( x \): Option A (linear function with varying slope).
To solve the problem of a parallel plate capacitor with half of the space filled with a dielectric material of constant \( K \), we will analyze the electric field and potential difference across the capacitor.
### Step-by-Step Solution:
1. **Understanding the Configuration**:
- A parallel plate capacitor consists of two plates separated by a distance \( d \).
- In this case, half of the space (i.e., \( d/2 \)) is filled with a dielectric material of constant \( K \), and the other half is air (or vacuum).
...
Similar Questions
Explore conceptually related problems
Parallel Plate Capacitors with and without Dielectric
A parallel plate capacitor of capacitance 10 muF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
Space between the plates of a parallel plate capacitor is filled with a dielectric whose dielectric constant varies with distance as per the relation: K(X)=K_(0)+lambdaX , ( lambda= constant, K_(0)= constant, X is perpendicular distance from one plate to a point inside dielectric). The capacitance C_(1) of this capacitor, would be related to its vacuum capacitance C_(0) per the relation (d = plate separation):
A parallel plate capacitar, of capacitance, 20 mu F , is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
The space between the plates of a parallel plate capacitor of capacitance C is filled with three dielectric slabs of identical size as shown in figure. If the dielectric constants of the three slabs are K_1 , K_2 and K_3 find the new capacitance.
The space between the plates of a parallel plate capacitor is completely filled with a material of resistivity 2 xx 10^(11)Omega -m and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the plates is 20nF . Find the leakage current if a potential difference 2500 V is applied across the capacitor.
The space between plates of a parallel plate capacitor is filled by a dielectric and it is charged and then battery is removed. Now dielectric slab is slowly drawn out of the capacitor parallel to the plates. The variation of the potential of capacitor with respect to the length of the dielectric plate drawn out is
Consider a parallel plate capacitor. When half of the space between the plates is filled with some dielectric material of dielectric constant K as Shown in Fig. (1) below, the capacitance is C_(1) . However , if the same dielectric material fills half the space as shown as shown in Fig. (2), the capacitance is C_(2) . Therefore, the ratio C_(1):C_(2) is
The space between the plates orf a parallel plate capacitor is completely filled with a meterail of resistaivity 2xx10^(11) Omegam and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the paltes is 20uF. Find the leakage current if a potential difference 2500 V is applied across the capacitor.
Recommended Questions
- Half of the space between the plates of a parallel plate capacitor is ...
Text Solution
|
- Two parallel plate capacitors, each of capacitance 40 muF, are connect...
Text Solution
|
- In figure half of the space between the plates of a parallel plate cap...
Text Solution
|
- In a parallel -plate capacitor, the plates are kept vertical. The uppe...
Text Solution
|
- The terminals of a battery of emf V are connected to the two plates of...
Text Solution
|
- Between the plates of a parallel plate capacitor a dielectric plate in...
Text Solution
|
- समान्तर प्लेट संधारित्र की प्लेटों के बीच के स्थान के आधे भाग में पराव...
Text Solution
|
- समान्तर प्लेट संधारित्र की दोनों प्लेटों के बीच की जगह को एक परावैद्यु...
Text Solution
|
- Half of the space between parallel plate capacitor is filled with a me...
Text Solution
|