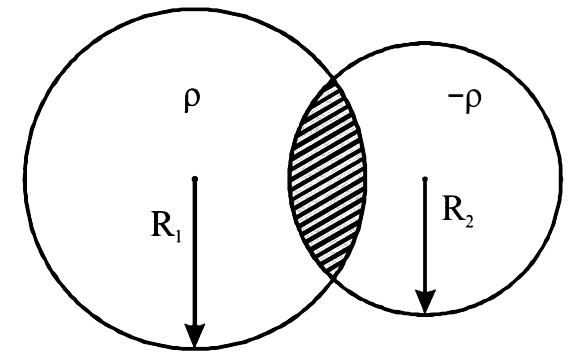
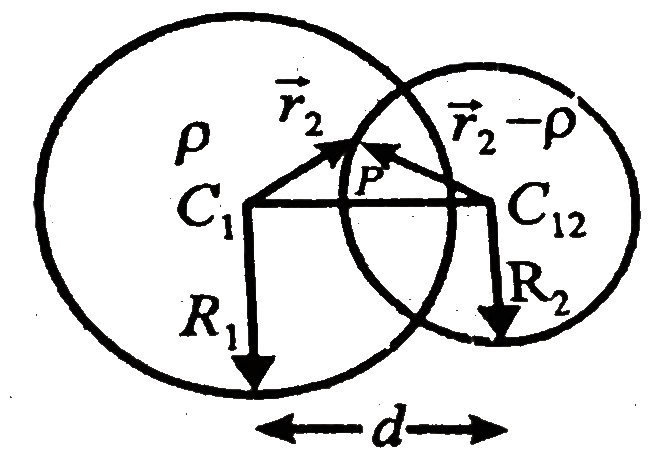A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two non-conducting spheres of radii R1 and R2 and carrying uniform vol...
Text Solution
|
- The region between two concentric spheres of radii 'a' and 'b', respec...
Text Solution
|
- There are two nonconducting spheres having uniform volume charge densi...
Text Solution
|
- A Uniformly charged solid non-conducting sphere of uniform volume char...
Text Solution
|
- Two non-conducting spheres of radii R(1) and R(2) and carrying uniform...
Text Solution
|
- दो अचालक R(1) तथा R(2) त्रिज्या वाले गोलों को क्रमशः +rho तथा -rho एकस...
Text Solution
|
- चार संकेंद्रित गोले A,B,C और D त्रिज्या क्रमशः a,2a,3a तथा 4a हैं। को...
Text Solution
|
- sigma and rho are surface and volume charge densities respectively of ...
Text Solution
|
- The region between two concentric spheres of radii 'a' and 'b', respec...
Text Solution
|