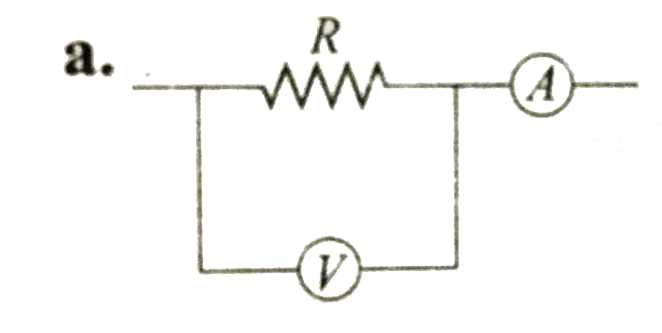
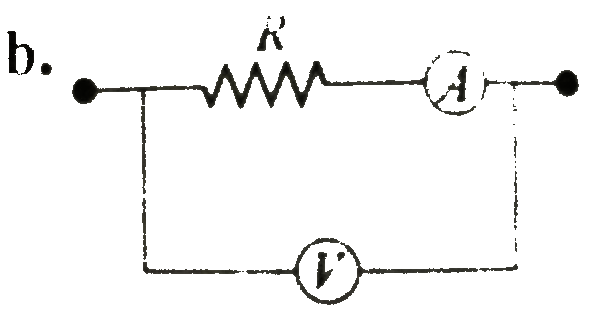
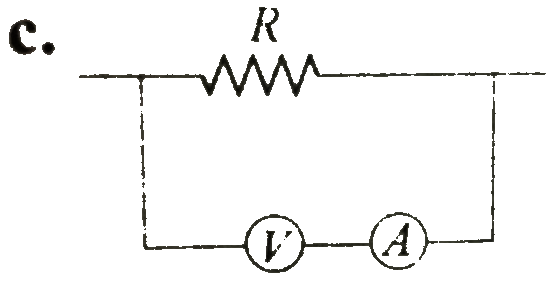
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Which of the following circuits gives the correct value of resistance,...
Text Solution
|
- In the circuit shown in Fig. 6.50, an idel ammeter and an ideal voltme...
Text Solution
|
- A voltmeter and an ammeter are connected in series to an ideal cell of...
Text Solution
|
- Which of the following circuits gives the correct value of resistance,...
Text Solution
|
- In the circuit shown the reading of ammeter and voltmeter are 4 A and ...
Text Solution
|
- In the, Ohm's law experiment ot find resistance of unknown resistor R,...
Text Solution
|
- In the circuit shown, A and V are ideal ammeter and voltmeter respecti...
Text Solution
|
- For the adjoining circuit diagram, the readings of ammeter and voltmet...
Text Solution
|
- In the adjoining circuit diagram, the readings of ammeter and voltmete...
Text Solution
|