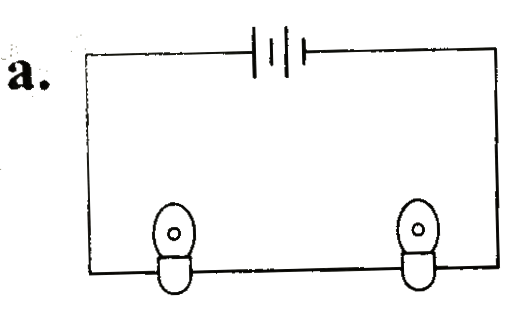
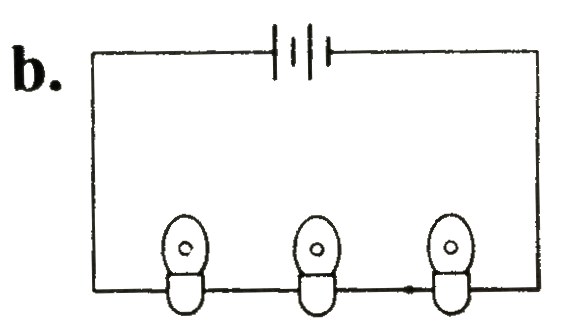
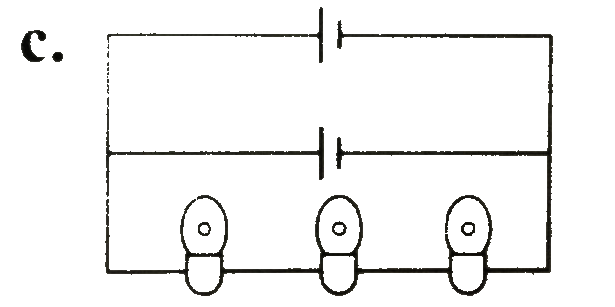
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the diagrams, all the light bulbs are identical, and all cells are ...
Text Solution
|
- All bulbs in the circuit shown in figure are identical. Which bulb glo...
Text Solution
|
- In the diagrams, all the right bulbs are identical, and all cells are ...
Text Solution
|
- In the circuit diagram, all the bulbs are identical. Which bulb will b...
Text Solution
|
- Assuming all bulbs are identical, rank the brightness of the bulbs, fr...
Text Solution
|
- In the diagrams, all light bulbs are identical and all emf sources are...
Text Solution
|
- All bulbs in figure below are identical which, bulbs light most bright...
Text Solution
|
- In the two circuits shown, all the light bulbs and batteries are ident...
Text Solution
|
- In which of the circuits given below above does the bulbs glow brighte...
Text Solution
|