Home
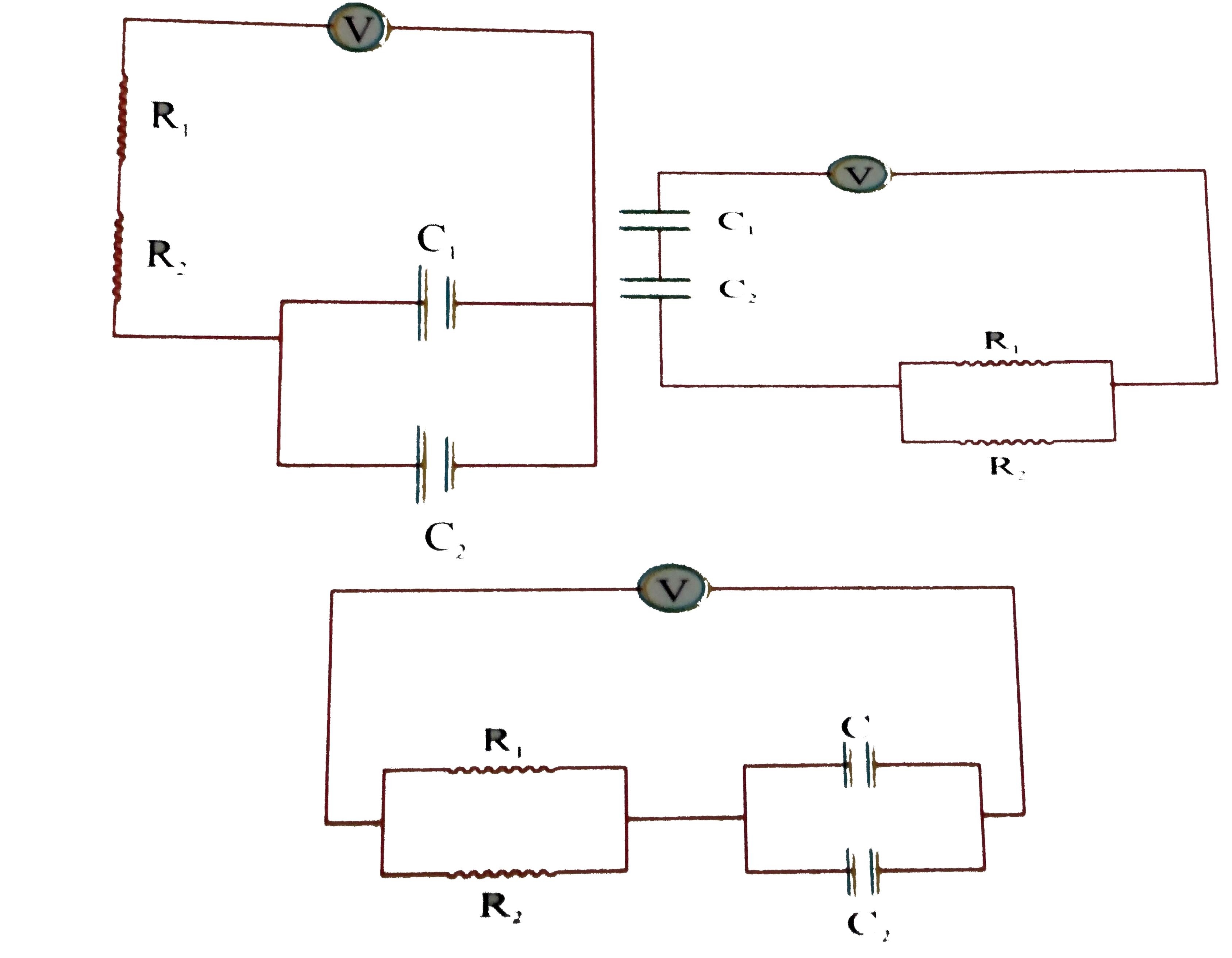
Class 12
PHYSICS
Find the time constant for the given RC ...


Find the time constant for the given RC circuits in correct order (in `mus`)
`R_(1)=1Omega,R_(2)=2Omega,C_(1)=4muF,C_(2)=2muF`

A

`18,4,8//9`

B

`18, 8//9,4`

C

`4,18, 8//9`

D

`4,8//9,18`

Text Solution

Verified by Experts

The correct Answer is:
B
b. We know that time constant of an RC circuit is RC. Find
equivalent resistance and capacitance in each case and then
determine the time constant.
Promotional Banner

Similar Questions

Explore conceptually related problems

The time constant for the given RC circuits in the correct order (in mus ). R_(1)=1Omega,R_(2)=2Omega,C_(1)=4muF,C_(2)=2muF

The potential difference in volt across the resistance R_(3) in the circuit shown in figure, is (R_(1)=15Omega,R_(2)=15Omega, R_(3)=30Omega, R_(4)=35Omega)

Initially the switch 'S' is open for a ling time. Now the switch 'S' is closed at t=0(R_(1)=2Omega, R_(2)=2Omega, C_(1)=1F and C_(2)=1F) Then

The equivalent capacity between A and B in the given circuit is (C_(1) =4muF,C_(2)=12 muF,C_(3)=8muF , C_(4)=4muF,C_(5)=8muF)

Find the change on the capacity C = 1muF in the circuit shown in the figure .

In the circuit shown in figure, R(1) = 1Omega, R_(2) = 2Omega, C_(1) = 1 muF, C_(2) = 2 muF and E = 6 V . Calculate charge on each capacitor in steady state

The resonant frequency of a series LCR circuit with L=2.0 H,C =32 muF and R=10 Omega is

In the circuit shown in fig. R_(1) = 10 Omega, R_(2) = 5 Omega, C_(1) = 1 muF, C_(2) = 2muF, and E =6V. Calculate the charge on each capactor in the stedy state.

In the given circuit. E_(1) = 6 volts, E_(2) = 2 volts, E_(3) = 6 volts R_(1) = 6OmegaR_( 2)=2Omega R_(3) = 4Oemga, R_(4) = 3Omega and C=5muF . Find the current in R_(3) and energy stored in the capacitor at steady state

(i) Find the equivalent capacitance of the combination shown in the figure (a), when C_(1)=2.0 muF,C_(2)=4.0 muF and C_(3) = 3.0 muF (ii) The input terminals A and B in Fig. (a) are connected to a battery of 12 V. Find the potential and the charge of each capacitor.