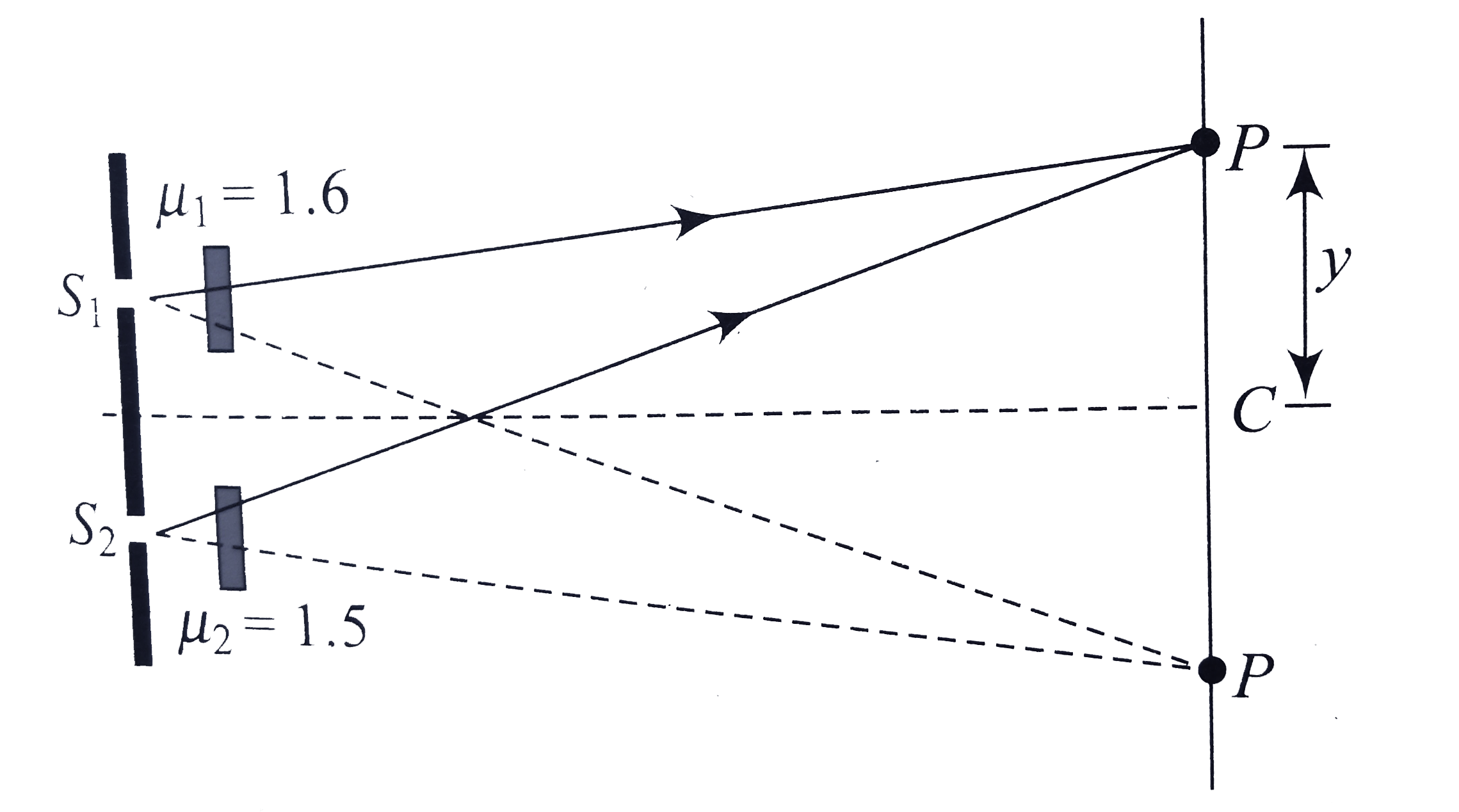
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CENGAGE PHYSICS ENGLISH-WAVE OPTICS-Subjective
- A monochromatic beam of light of 6000 Å is used in YDSE set-up. The tw...
Text Solution
|
- A double slit of separation 1.5 mm is illuminated by white light (betw...
Text Solution
|
- In figure S is a monochromatic source of light emitting light of wavel...
Text Solution
|
- In the Young's double-slit experiment, the amplitude os source S(1) is...
Text Solution
|
- Figure shows a narrow slit S illuminated b a monochromatic light of wa...
Text Solution
|
- In Young's double-slit experiment, a point source is placed on a solid...
Text Solution
|
- In YDSE, the sources is red ligth of wavelength 7 xx 10^(-7) m. When a...
Text Solution
|
- Figure shows a modified Fresnel biprism experiment with monochromatic ...
Text Solution
|
- Interference fringes are produced by a double slit arrangement and a...
Text Solution
|
- In YDSE, find the thickness of a glass slab (mu=1.5) which should be...
Text Solution
|
- Bichromatic light is used in YDSE having wavelengths lambda1 = 400 n...
Text Solution
|