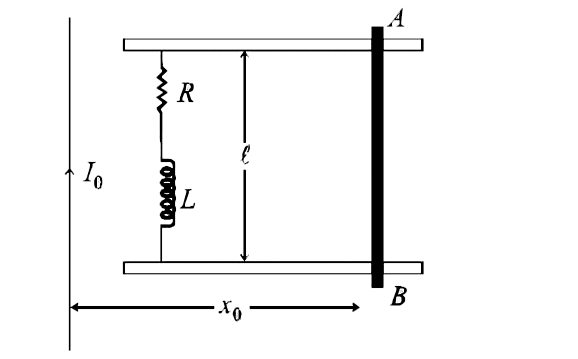
a. When bar `AB` slider away, the magneic force acts on free electrons along negative Y-axis, so electrons move from end `A` to end `B`, making end `A` at positive potential relative to end `B`. So current in the circuit will flow from `B` to `A` as shows.
Let `epsilon` be the induced emf According to kirchhoff's second law,
`-Ri - L(di)/(dt) + epsilon = 0 rArr epsilon = Ri + L (di)/(dt)`
But `epsilon = (d phi)/(dt)` (numerically)
`:. (d phi)/(dt) = Ri + L (di)/(dt)` (i)
This i sthe required relation.
b. Equation (i) can be expressed as
`d phi = Ridt + L di rArr d phi R dq + ldi`
Integrating, we get
`int_(0)^(T) d phi = R int_(0)^(q) dq + L int_(0)^(i_(1)) di`
`[phi]_(t = 0)^(T) = Rq + Li_(1)`
`:.` Charge flows from `t = 0` to `t = T` will be
`q = (1)/(R) [phi(T) - phi(0)] - (Li_(1))/(R)` (ii)
Change in flux during the displacement of bar from `x = x_(0)` to `x = 2 x_(0)` in time `T` is
`phi(T) - phi(0) = int_(x_0)^(2_(x_0)) BdA = int_(x_0)^(2_(x_0)) (mu_(0)I_(0))/(2 pi x) ldx`
`= (mu_(0)I_(0)l)/(2 pi) log_(e) 2` (iii)
`:.` From Eq.(ii), charge flows
`q = (mu_(0)I_(0)l)/(2 piR) log_(e) 2 - (Li_(1))/(R)` (iv)
c. The equation of decay of current in an `LR` circuit is given by
`i = i_(0)e^(-Rt//L)` (v)
Given `i = (i_(1))/(4), i_(0) = i_(1), t = 2T - T = T`
`:.` Substituting these values in Eq.(v), we get
`(i_(1))/(4) = i_(1) e^(-RT//L) rArr e^(-RT//L) = (1)/(4)`
or `(RL)/(L) = log_(e)4 :. (L)/(R) = (T)/(log_(e) 4)`