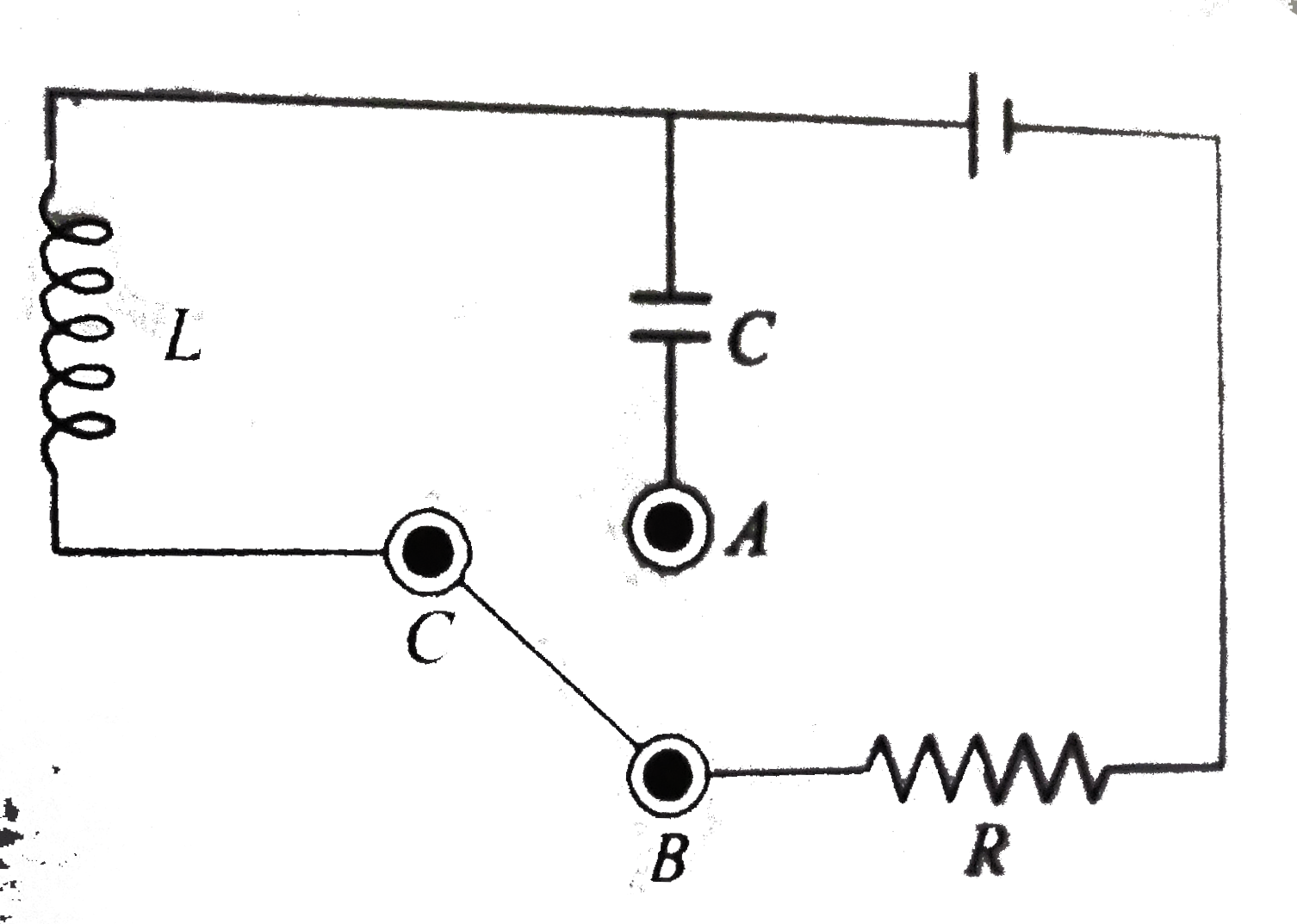
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
INDUCTANCE
CENGAGE PHYSICS ENGLISH|Exercise Exercises (single Correct )|65 VideosINDUCTANCE
CENGAGE PHYSICS ENGLISH|Exercise Exercises (multiple Correct )|7 VideosINDUCTANCE
CENGAGE PHYSICS ENGLISH|Exercise Exercise 4.1|24 VideosHEATING EFFECT OF CURRENT
CENGAGE PHYSICS ENGLISH|Exercise Thermal Power in Resistance Connected in Circuit|27 VideosMAGNETIC FIELD AND MAGNETIC FORCES
CENGAGE PHYSICS ENGLISH|Exercise Multiple Correct Answer type|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-INDUCTANCE-Exercises (subjective)
- In Fig. a uniform magnetic field decrease at a constant rate dB//dt = ...
Text Solution
|
- In the circuits shows in S(1) and S(2) are switches. S(2) remains clos...
Text Solution
|
- In Fig a rod of length l and mass m moves with an intial velocity u on...
Text Solution
|
- A 1.00 mH inductor and a 1.00muF capacitor are connected in series. Th...
Text Solution
|
- Two capacitors of capacitances 2C and C are connected in series with a...
Text Solution
|
- Switch S is cloesd in the circuit at time t = 0. Find the current thro...
Text Solution
|
- In the circuit shows in Fig the capacitor is initially uncharged and t...
Text Solution
|