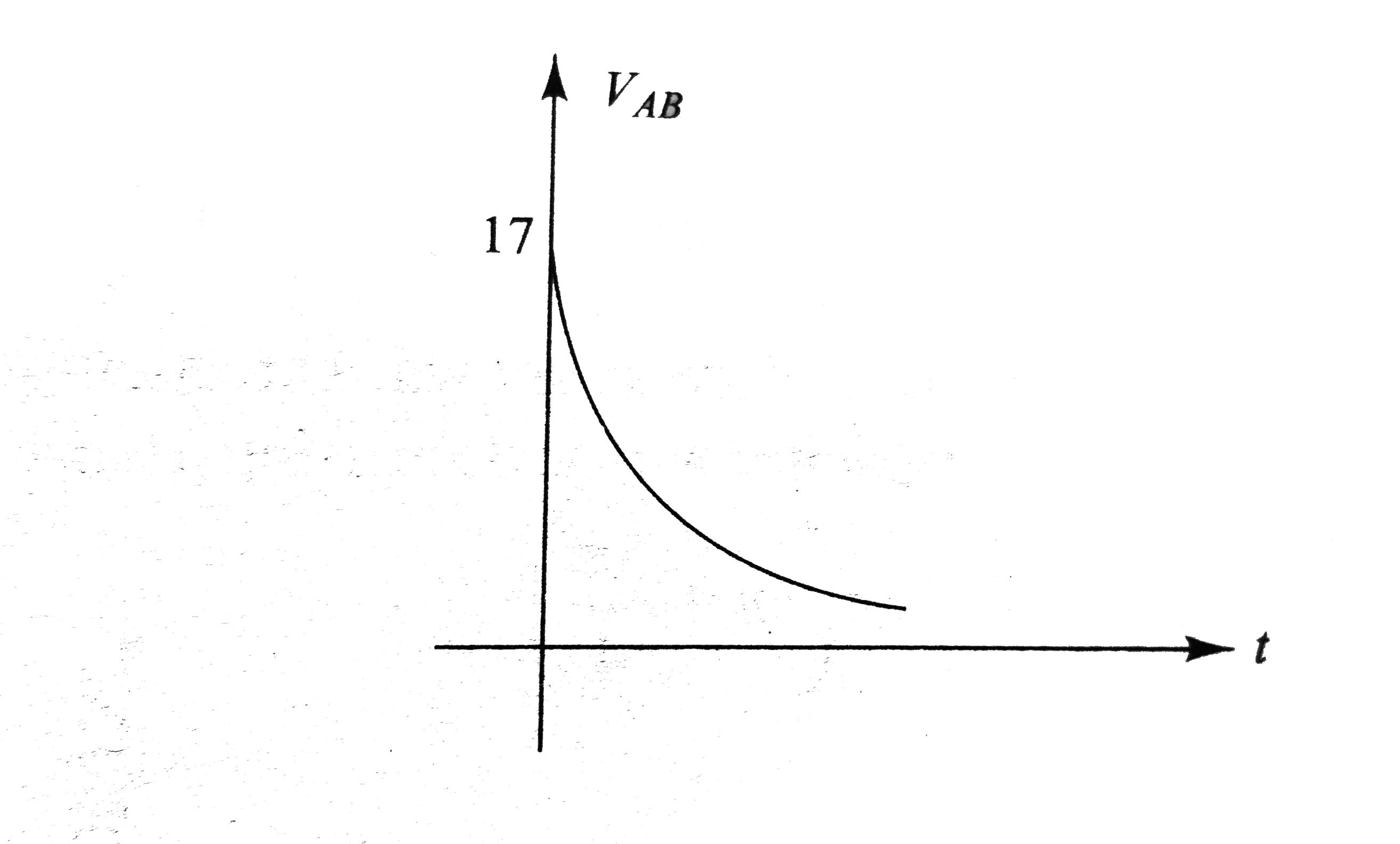
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
INDUCTANCE
CENGAGE PHYSICS ENGLISH|Exercise Exercises (integer)|8 VideosINDUCTANCE
CENGAGE PHYSICS ENGLISH|Exercise Archives (fills In The Blanks)|3 VideosINDUCTANCE
CENGAGE PHYSICS ENGLISH|Exercise Exercises (assertion-reasoning)|2 VideosHEATING EFFECT OF CURRENT
CENGAGE PHYSICS ENGLISH|Exercise Thermal Power in Resistance Connected in Circuit|27 VideosMAGNETIC FIELD AND MAGNETIC FORCES
CENGAGE PHYSICS ENGLISH|Exercise Multiple Correct Answer type|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-INDUCTANCE-Exercises (linked Compreshension)
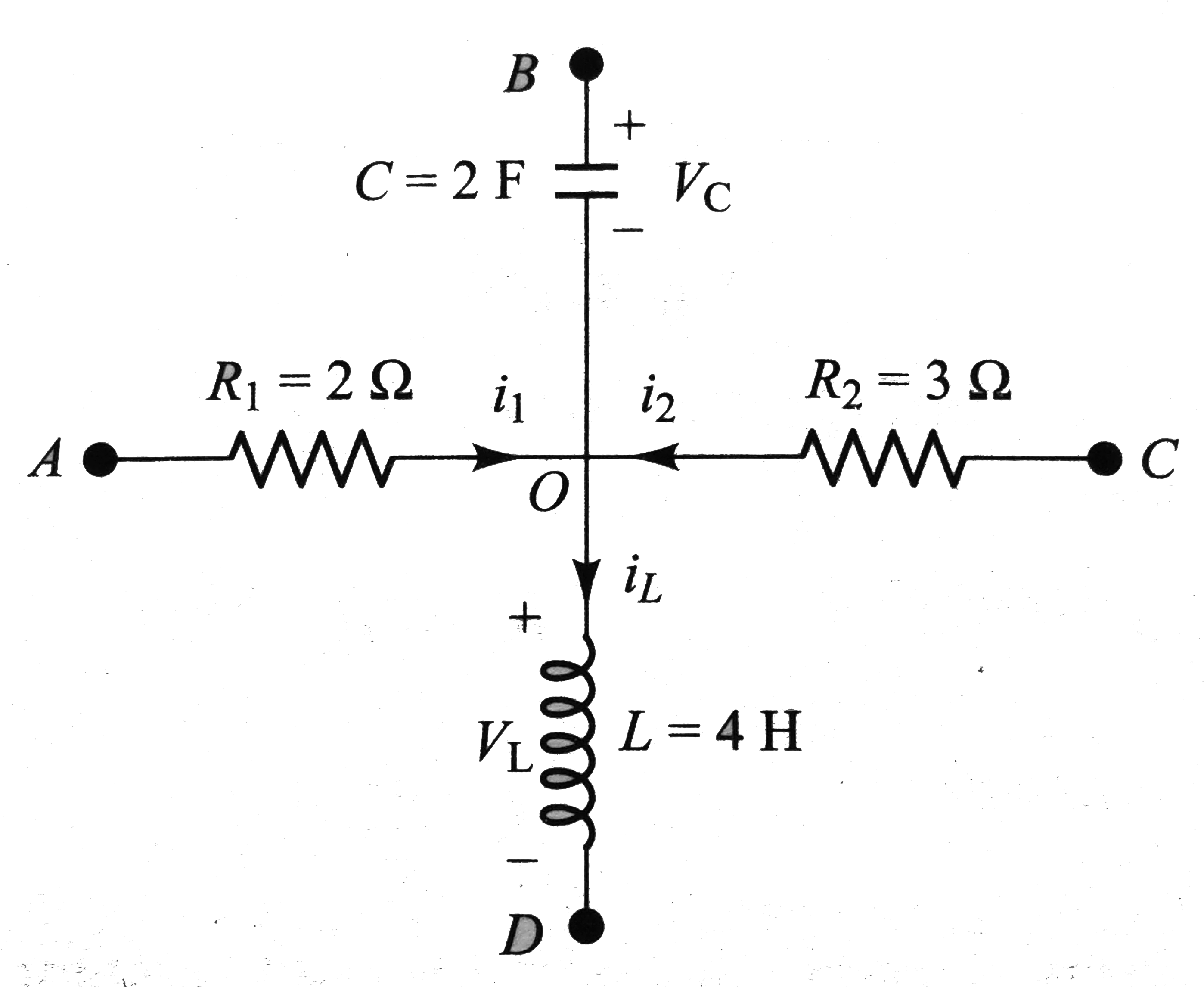
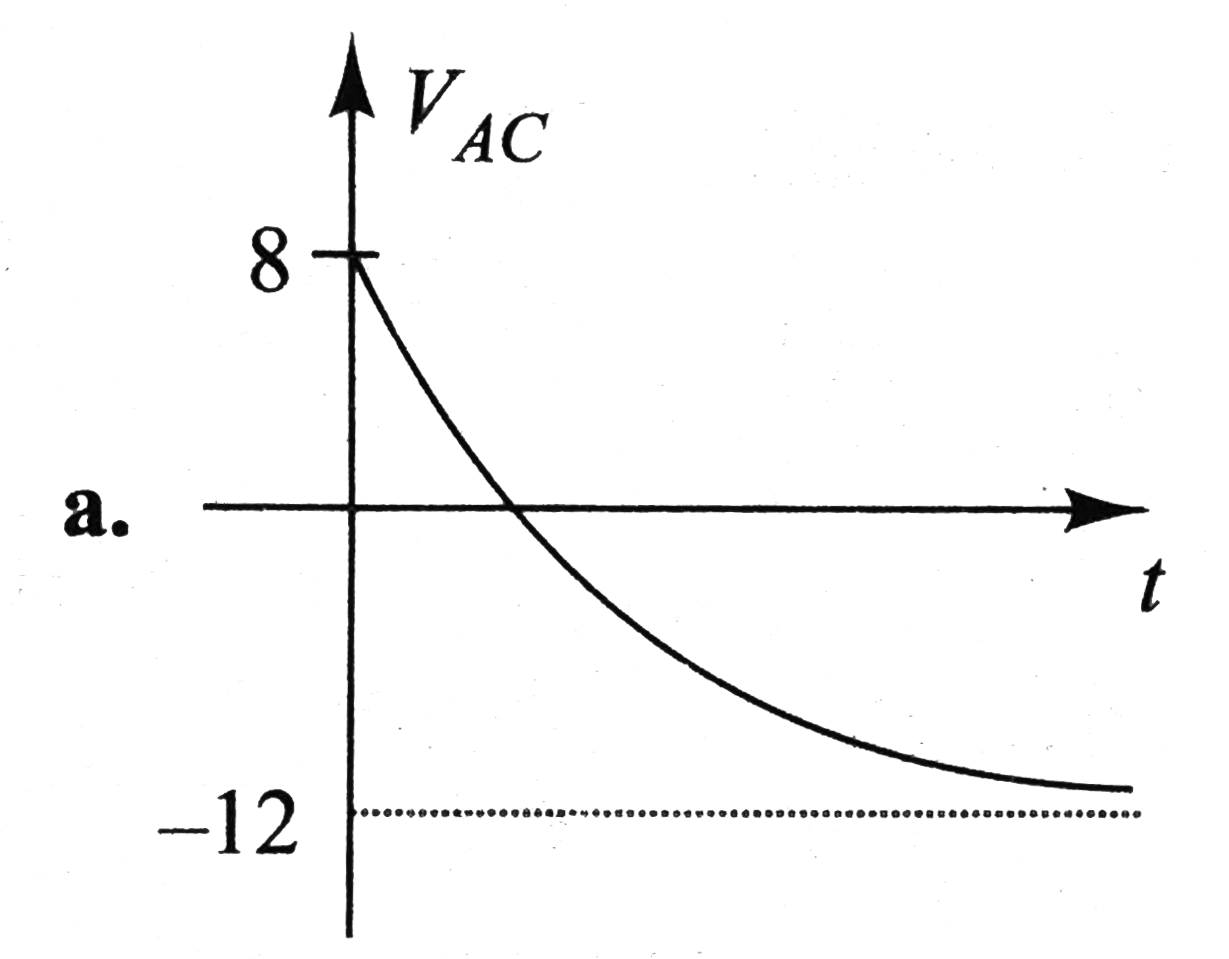
- In Fig i(1) = 10e^(-2t) A, i(2) = 4 A, and V(C) = 3e^(-2t) V. The...
Text Solution
|
- In the Figure shown i1=10e^(-2t) A, i2=4A and VC=3e^(-2t)V. Determine...
Text Solution
|
- In Fig i(1) = 10e^(-2t) A, i(2) = 4 A, and V(C) = 3e^(-2t) V. th...
Text Solution
|
- In the Figure shown i1=10e^(-2t) A, i2=4A and VC=3e^(-2t)V. Determine...
Text Solution
|
- In Fig i(1) = 10e^(-2t) A, i(2) = 4 A, and V(C) = 3e^(-2t) V. Th...
Text Solution
|
- In the circuit shows (Fig.) switches S(1) and S(3) have been closed fo...
Text Solution
|
- In the circuit shows (Fig.) switches S(1) and S(3) have been closed fo...
Text Solution
|
- In the circuit shows (Fig.) switches S(1) and S(3) have been closed fo...
Text Solution
|
- In the given (Fig.) all the symbols have their usual meanings. At t = ...
Text Solution
|
- In the given (Fig.) all the symbols have their usual meanings. At t = ...
Text Solution
|
- In the circuit shows in Fig E = 15 V, R(1) = 1Omega, R(2) = 1 Omega, R...
Text Solution
|
- In the circuit shows in Fig E = 15 V, R(1) = 1Omega, R(2) = 1 Omega, R...
Text Solution
|
- In the circuit shows in Fig E = 15 V, R(1) = 1Omega, R(2) = 1 Omega, R...
Text Solution
|
- In the given at t = 0, switch S is closed. The current through th...
Text Solution
|
- In the given at t = 0, switch S is closed. The energy stored in t...
Text Solution
|
- In the given at t = 0, switch S is closed. The energy stored in t...
Text Solution
|
- In Fig. there is a frame consisting of two square loops having resist...
Text Solution
|
- In Fig. there is a frame consisting of two square loops having resist...
Text Solution
|
- In Fig. there is a frame consisting of two square loops having resist...
Text Solution
|
- there in no current part of this circuit for time t lt o. Switch S is ...
Text Solution
|