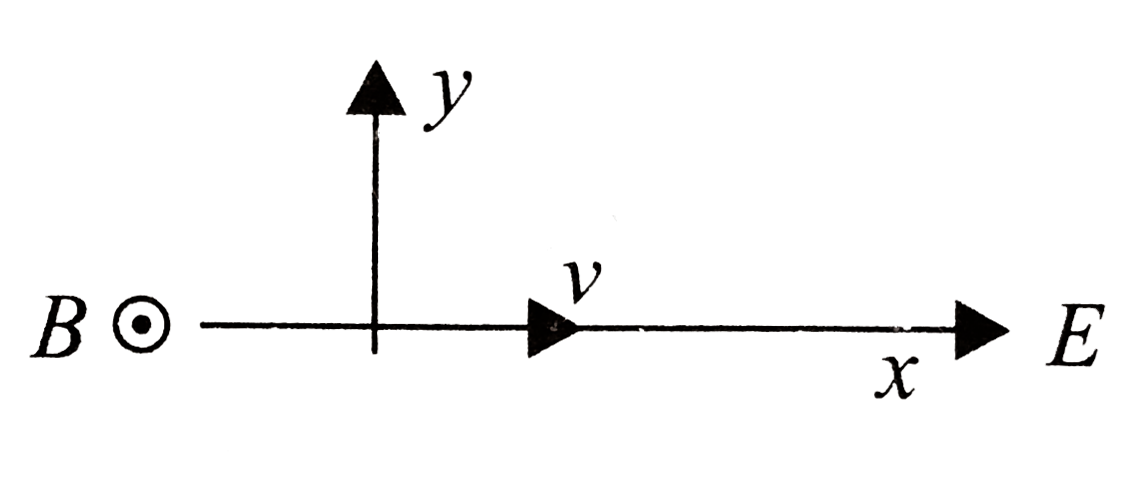A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MISCELLANEOUS VOLUME 5
CENGAGE PHYSICS ENGLISH|Exercise Linked Comprehension|84 VideosMISCELLANEOUS VOLUME 5
CENGAGE PHYSICS ENGLISH|Exercise Integer|12 VideosMISCELLANEOUS VOLUME 5
CENGAGE PHYSICS ENGLISH|Exercise Integer|12 VideosMISCELLANEOUS VOLUME 3
CENGAGE PHYSICS ENGLISH|Exercise True and False|3 VideosNUCLEAR PHYSICS
CENGAGE PHYSICS ENGLISH|Exercise ddp.5.5|14 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-MISCELLANEOUS VOLUME 5-Multiple Correct
- A particle is released from the origin with a velocity vhate(i). The e...
Text Solution
|
- A charged particle of specific charge s passes undeviated through regi...
Text Solution
|
- A proton is fired from origin with velocity V=v(0)hatJ+v(0)hatK in a ...
Text Solution
|
- H^(+), He^(+) and O^(2+) ions having same kinetic energy pass through ...
Text Solution
|
- A beam of electrons moving with a momentum p enters a uniform magnetic...
Text Solution
|
- A plane rectangular loop is placed in a magnetic field. The emf induce...
Text Solution
|
- Figure shows cross section of two large parallel metal sheets carrying...
Text Solution
|
- For the given electromagnetically coupled circuits: (S is initially in...
Text Solution
|
- In the circuit, a battery of emf E, a resistance R and inductance coil...
Text Solution
|
- When current (I) in R-L series circuit becomes constant, where L is a ...
Text Solution
|
- A charged particle enters into a space and continues to move undeflect...
Text Solution
|
- A variable voltage V = 2t is applied across an inductor of inductance ...
Text Solution
|
- There are two coils A and B as shown in Fig.
Text Solution
|
- The current in a certain circuit varies with time as shown in figure. ...
Text Solution
|
- For the circuit shown in Fig. the emf of the generator is E. The curre...
Text Solution
|
- A semicircle conducting ring of radius R is placed in the xy plane, as...
Text Solution
|
- A bar magnet is moved along the axis of a copper ring placed far away ...
Text Solution
|
- Two long parallel wires, AB and CD, carry equal currents in opposite d...
Text Solution
|
- L is a circular loop (in y-z plane) carrying an anticlockwise current....
Text Solution
|
- A straight wire carrying current is parallel to the y-axis as shown in...
Text Solution
|