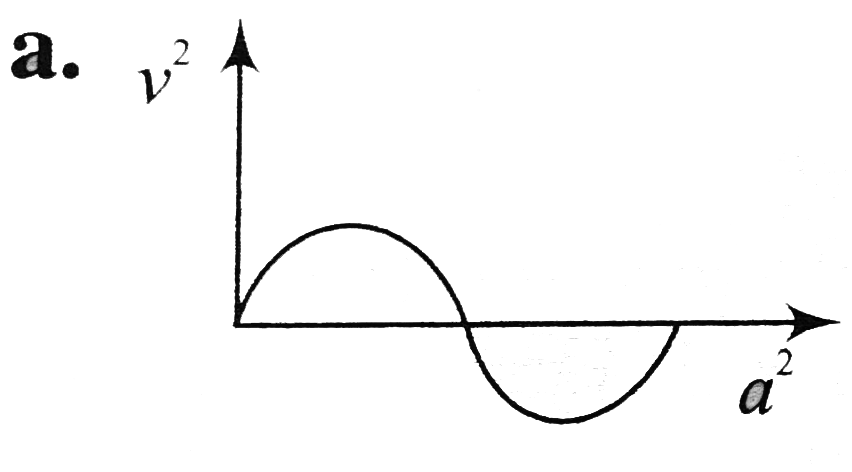
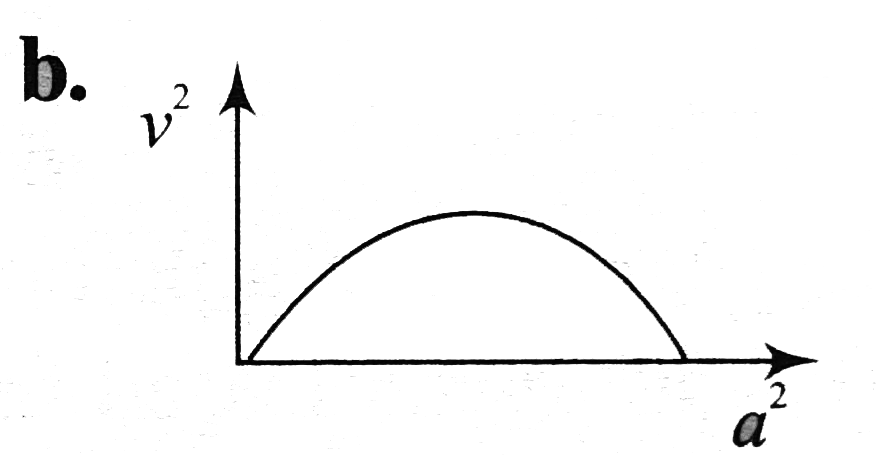
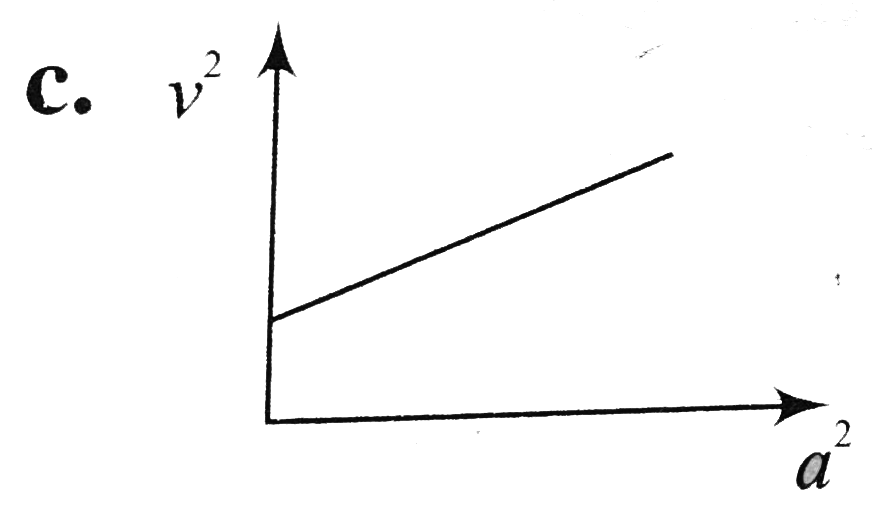
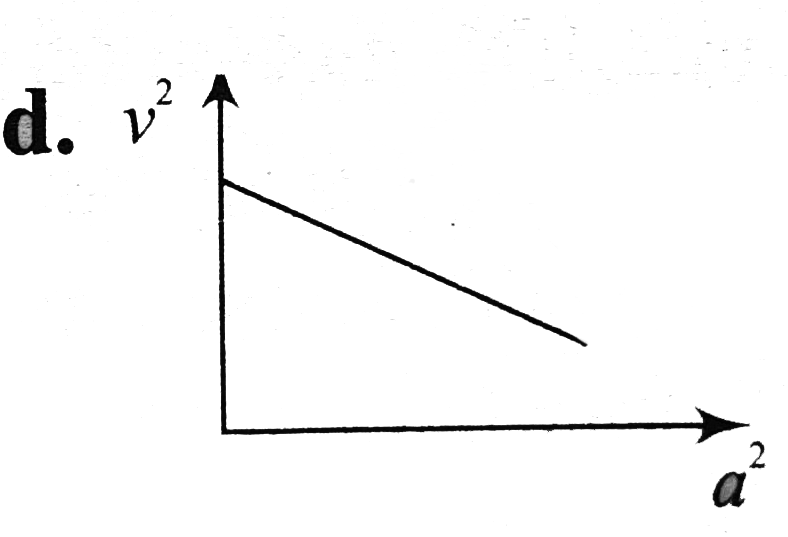
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS ENGLISH|Exercise Multiple Correct|35 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS ENGLISH|Exercise Assertion Reasoning|6 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS ENGLISH|Exercise Subjective|21 VideosKINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
CENGAGE PHYSICS ENGLISH|Exercise Interger|11 VideosMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS ENGLISH|Exercise Interger type|3 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Single Correct
- The osciallations represented by curve 1 in the graph are expressed by...
Text Solution
|
- Graph shows the x(t) curves for the three experiments involving a part...
Text Solution
|
- The acceleration of a particle is a = - 100x + 50. It is released from...
Text Solution
|
- In the above question, the speed of the particle at origin will be:
Text Solution
|
- A particle performs SHM of amplitude A along a straight line. When it ...
Text Solution
|
- A uniform pole length l = 2l, is laid on a smooth horizontal table as ...
Text Solution
|
- A small mass executes linear SHM about O with amplitude a and period T...
Text Solution
|
- The period of a particle executing SHM is 8 s . At t=0 it is at the me...
Text Solution
|
- A particle performs SHM with a period T and amplitude a. The mean velo...
Text Solution
|
- A graph of the square of the velocity against the square of the accele...
Text Solution
|
- A plank with a small block on top of it is under going vertical SHM. I...
Text Solution
|
- The potential energy of a harmonic oscillator of mass 2 kg in its mean...
Text Solution
|
- A spring mass system preforms S.H.M if the mass is doubled keeping amp...
Text Solution
|
- A particle of mass m moves in a one dimensional potential energy U(x)=...
Text Solution
|
- A particle of mass m moves in the potential energy U shoen above. The ...
Text Solution
|
- The displacement of a body executing SHM is given by x=A sin (2pi t+pi...
Text Solution
|
- Two particles are executing SHM in a straight line. Amplitude A and th...
Text Solution
|
- System is shown in the figure. Velocity of sphere A is 9 (m)/(s). Find...
Text Solution
|
- A particle is subjected to two mutually perpendicular simple harmonic ...
Text Solution
|
- Two simple harmonic motions y(1) = Asinomegat and y(2) = Acosomegat ar...
Text Solution
|