Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-TRAVELLING WAVES-Integer
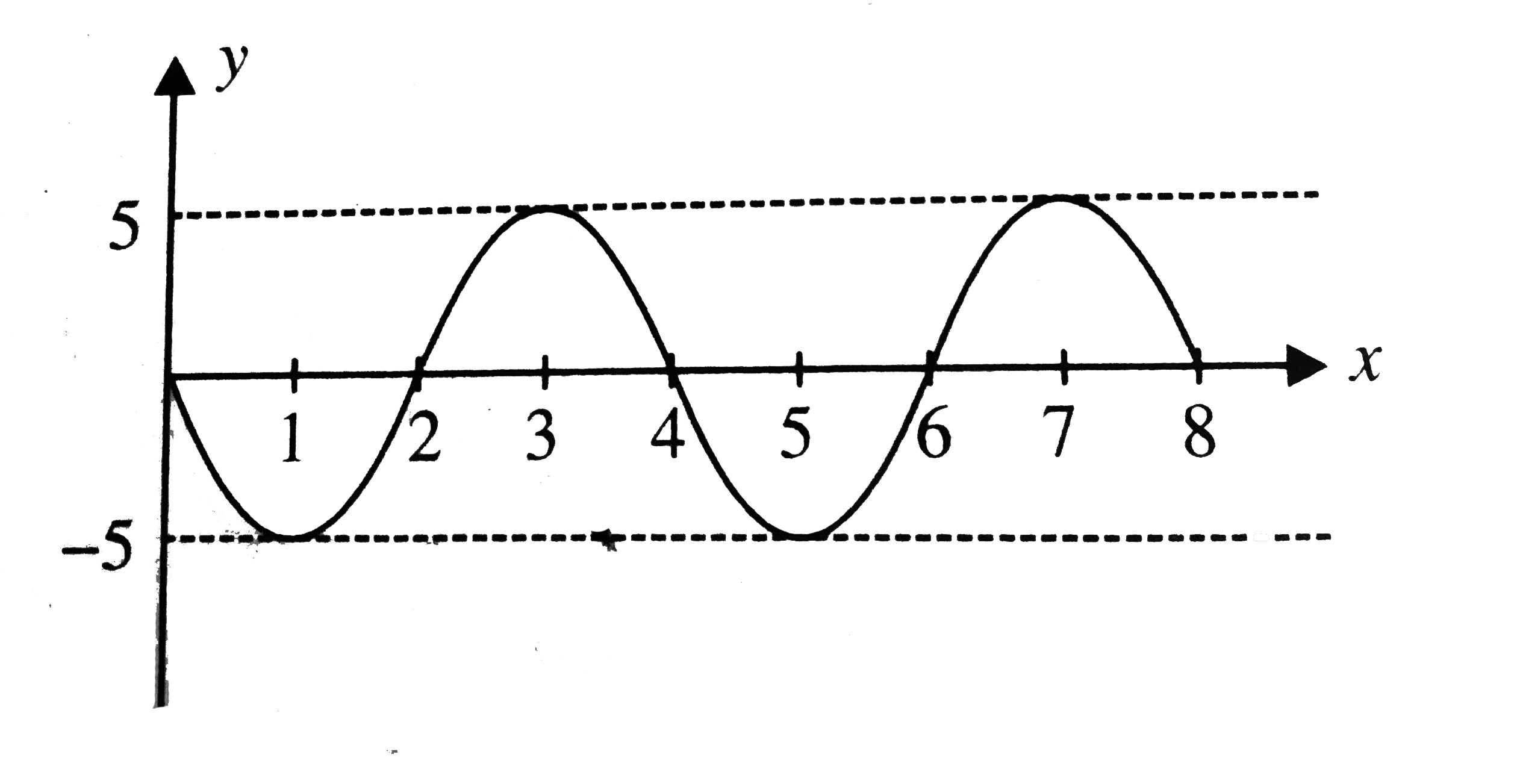
- Shows the shape of a progressive wave at time t=0. after a time t=(1)/...
Text Solution
|
- The speed of a transverse wave going on a wire having a length 50 cm ...
Text Solution
|
- A wave pulse passing on a string with speed of 40cms^-1 in the negativ...
Text Solution
|
- A particle on a stretched string supporting a travelling wave, takess ...
Text Solution
|
- A string of length 20 cm and linear mass density 0.4 g//cm is fixed a...
Text Solution
|
- A string of length 40 cm and weighing 10 g is attached to a spring at ...
Text Solution
|
- A 4.0 kg block is suspended from the ceiling of an elevator through a ...
Text Solution
|
- A plane progressive wave is given by x=(40 cm) cos(50pit-0.02piy) wher...
Text Solution
|
- A travelling wave pulse is given by y=(0.8)/((3x^(2)+12xt+12t^(2)+4...
Text Solution
|
- An ant with mass m is standing peacefully on top of a horizontal, stre...
Text Solution
|
 .
.