A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The resultant of two vectors vecA and vecB is perpendicular to the vec...
Text Solution
|
- The resultant of two vectors vecA and vecB is perpendicular to the vec...
Text Solution
|
- vecA and vecB are two vectors of equal magnitude and theta is the angl...
Text Solution
|
- The resultant of two vectors vecA and vecB is perpendicular to vecA an...
Text Solution
|
- if veca,vecb and vecc are mutally perpendicular vectors of equal magni...
Text Solution
|
- The resultant of the vectors A and B is perpendicular to the vector A ...
Text Solution
|
- Two vectors vecA" and "vecB have equal magnitudes. If magnitude of vec...
Text Solution
|
- The resultant of two vectors vecA and vecb is perpendicular to the vec...
Text Solution
|
- दो सदिशों vecA तथा vecB का परिणामी सदिश vecA के लम्बवत है तथा इसका परि...
Text Solution
|
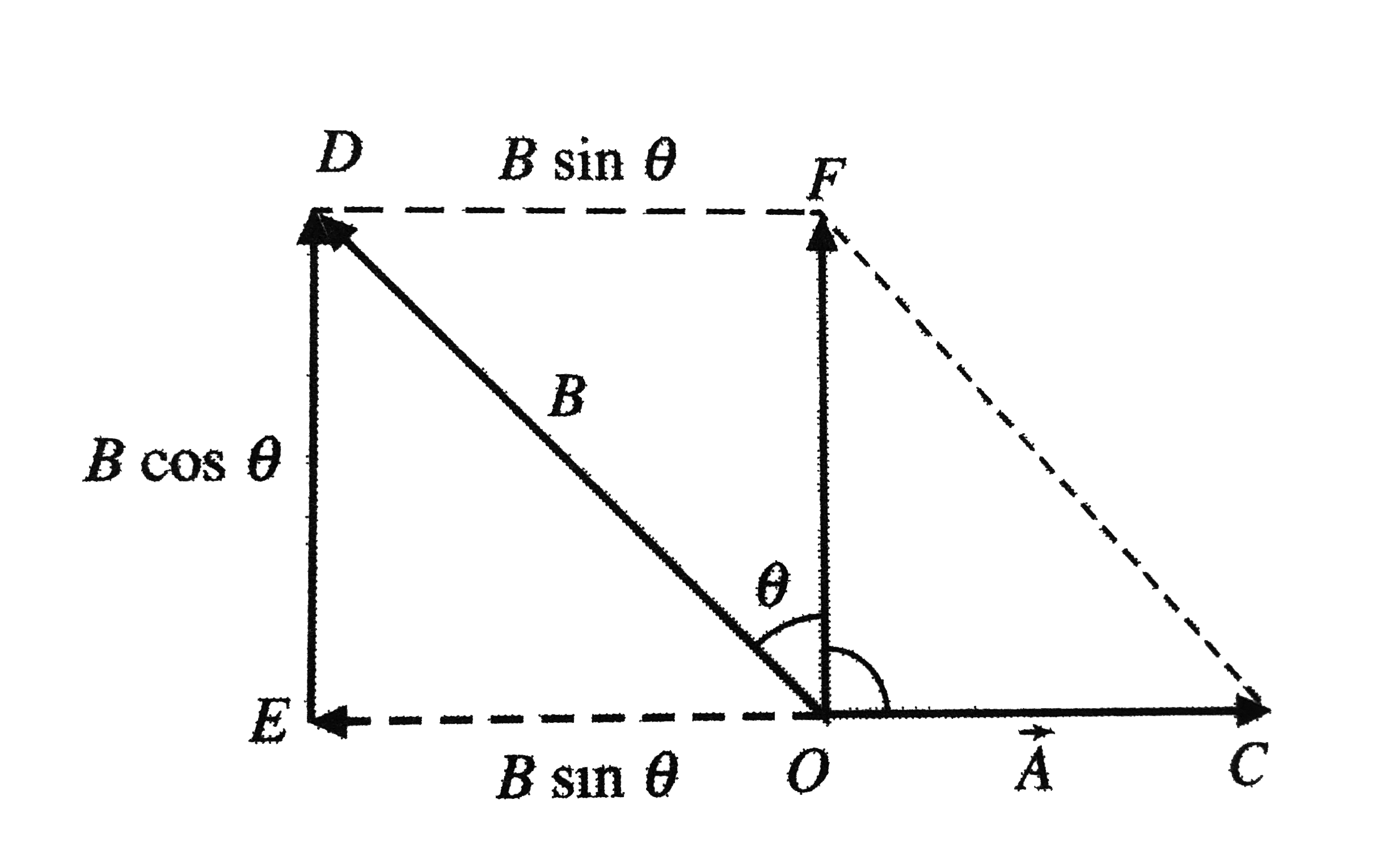 .
.