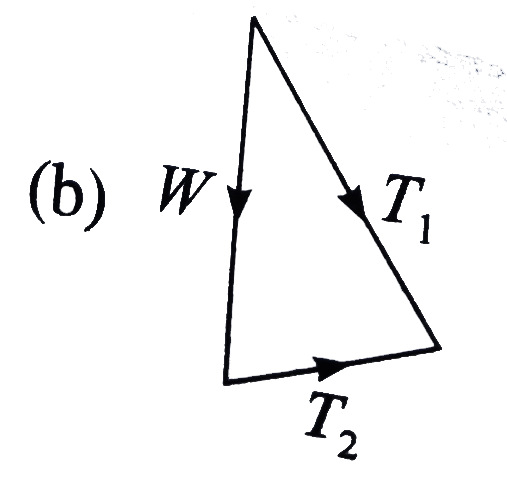A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
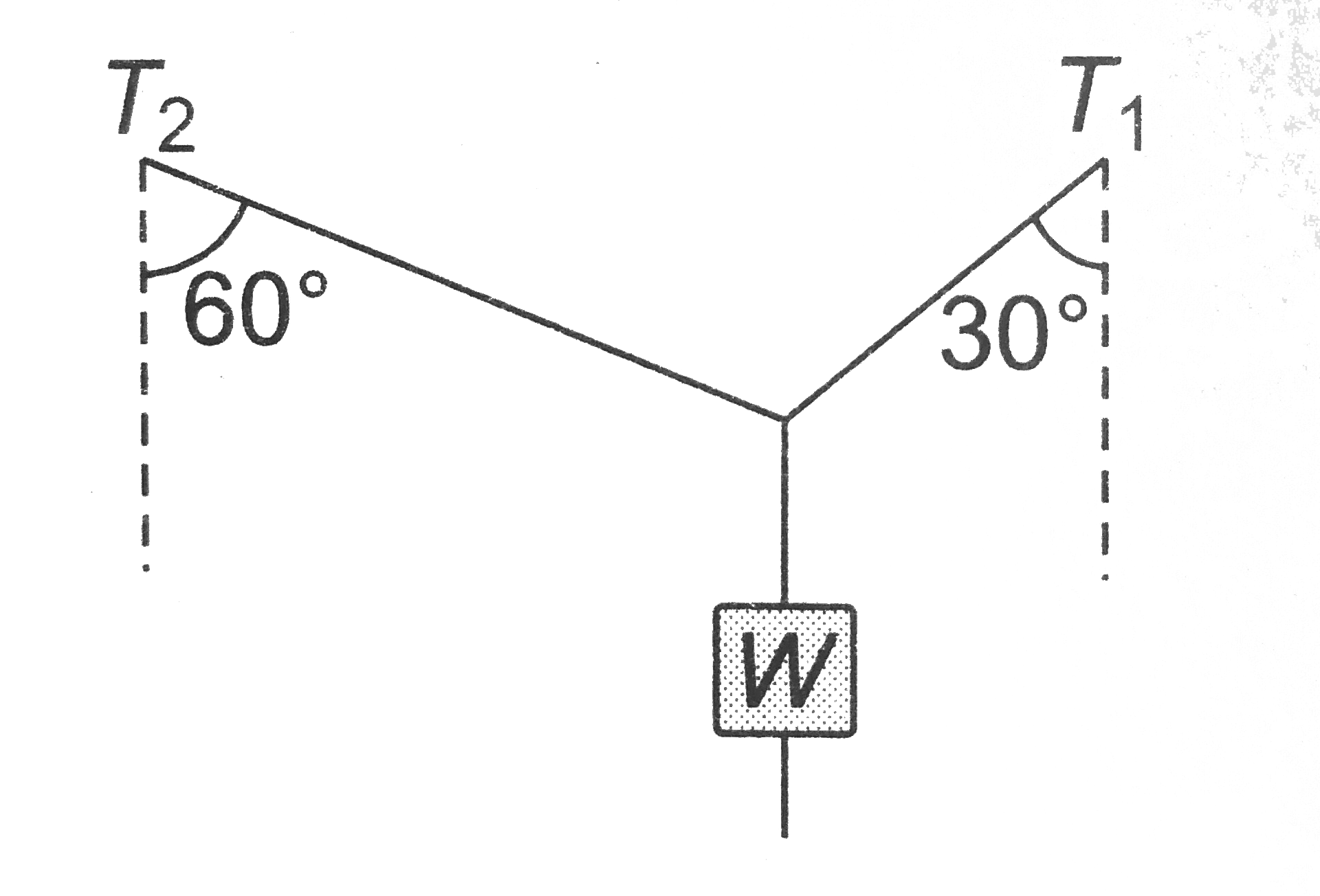
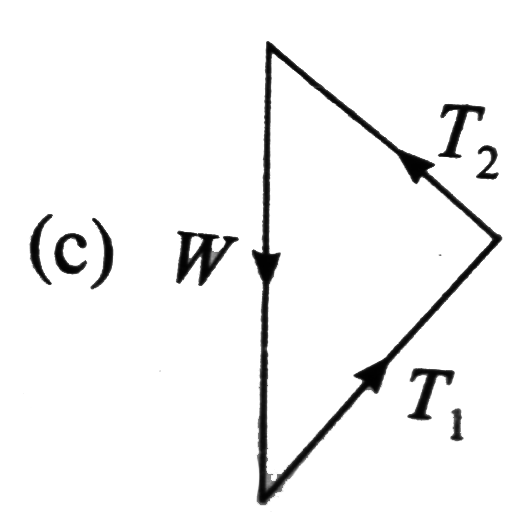
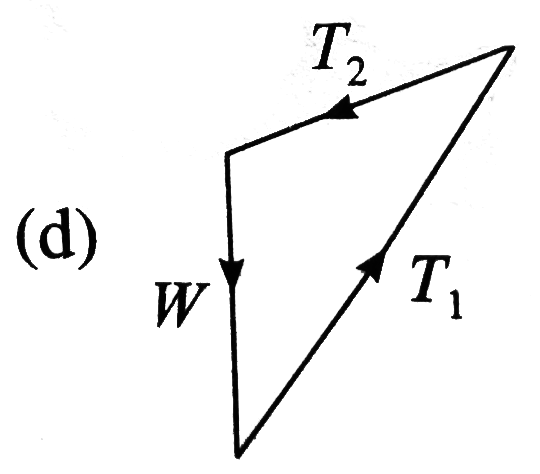
- A weight W is supported by two strings inclined at 60^(@) and 30^(@) t...
Text Solution
|
- Determine the tensions T(1) and T(2) in the string as shown in figure.
Text Solution
|
- As shown in figure the tension in the horizontal cord is 30 N. The wei...
Text Solution
|
- A weight w is supported by two strings anclined at 60^(@) and 30^(@) t...
Text Solution
|
- Determine the tension T(1) and T(2) in the strings shown in Fig.
Text Solution
|
- A system is at rest as shown in figure. The tension in the string in T...
Text Solution
|
- A block of weight W is supported by three strings as shown in figure. ...
Text Solution
|
- Determine the tension T(1) and T(2) in the strings
Text Solution
|
- Determine the tension T(1) and T(2) in the strings
Text Solution
|