Home
Class 12
PHYSICS
Two weights W1 and W2 in equilibrius and...


Two weights `W_1` and `W_2` in equilibrius and at rest are suspended as shown in figure. Then the ratio `(W_1)/(W_2)` is:

A

`(5)/(4)`

B

`(4)/(5)`

C

`(8)/(5)`

D

none of these

Text Solution

Verified by Experts

The correct Answer is:
A

Resolving forces at point A along string AB
`w_1cos37^@=w_2`
`(w_1)/(w_2)=(5)/(4)`
Promotional Banner

Similar Questions

Explore conceptually related problems

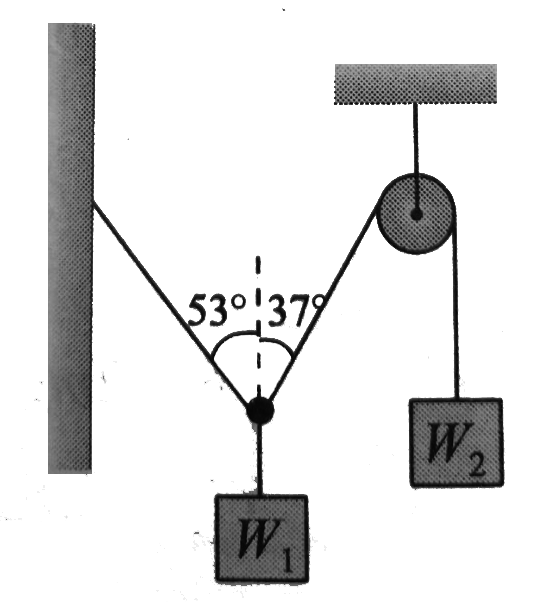
Two weights W_(1) and W_(2) in equilibrium and at rest, are suspended as shown in figure. Then the ratio (W_(1))/(W_(2)) is :

Find the resultant of the three vectors shown in figure (2W1). .

A 100 W bulb B_1 , and two 60 W bulb B_2 and B_3 , are connected to a 250 V source, as shown in figure. Now W_1, W_2 and W_3 are the output powers of the bulbs B_1, B_2 and B_3 , respectively. Then

A 100 W bulb B_(1) and two 60 W bulbs B_(2) and B_(3) , are connected to a 250V source, as shown in the figure now W_(1),W_(2) and W_(3) are the output powers of the bulbs B_(1),B_(2) and B_(3) respectively then

A 100 W bulb B_(1) and two 60 W bulbs B_(2) and B_(3) , are connected to a 250V source, as shown in the figure now W_(1),W_(2) and W_(3) are the output powers of the bulbs B_(1),B_(2) and B_(3) respectively then

A 5 V battery with internal resistance 1 Omega and a 2 V battery with internal resistance 0.5 Omega are connected to a 3 Omega resistor as shown in the figure.The current in the 3 Omega resistor is

A given mass of a gas expands from the state A to the state B by three paths 1,2 and 3 as shown in the figure, If W_(1),W_(2) and W_(3) respectively be the work done by the gas along the three paths then

A body of weight w_1 is suspended from the ceiling of a room through as chain of weight w_2 . The ceiling pulls the chain by a force

A body of weight W is suspended by a string It is pulled aside with a horizontal force of 2W and held at rest. The tension in it is

Two planets of radii R_(1) and R_(2 have masses m_(1) and M_(2) such that (M_(1))/(M_(2))=(1)/(g) . The weight of an object on these planets is w_(1) and w_(2) such that (w_(1))/(w_(2))=(4)/(9) . The ratio R_(1)/R_(2)