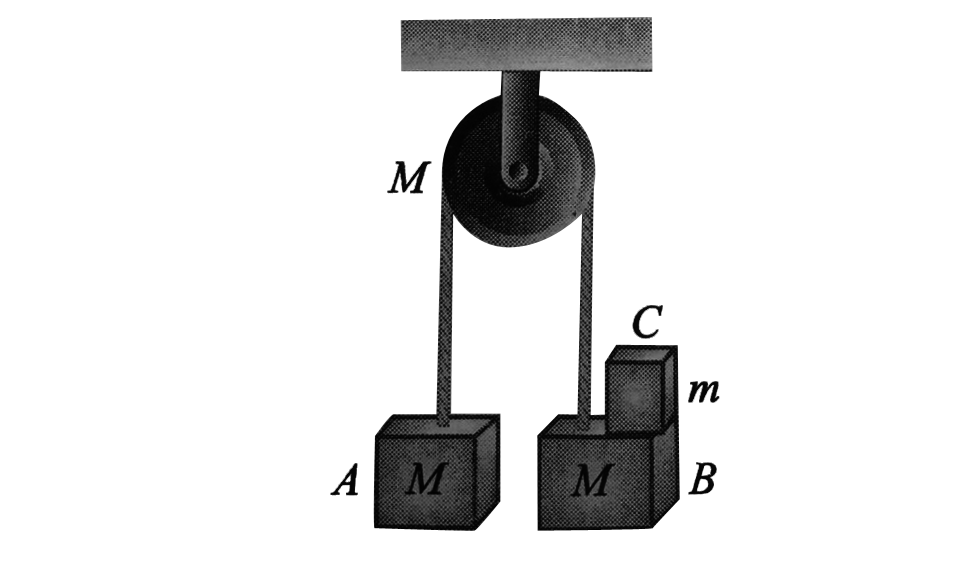
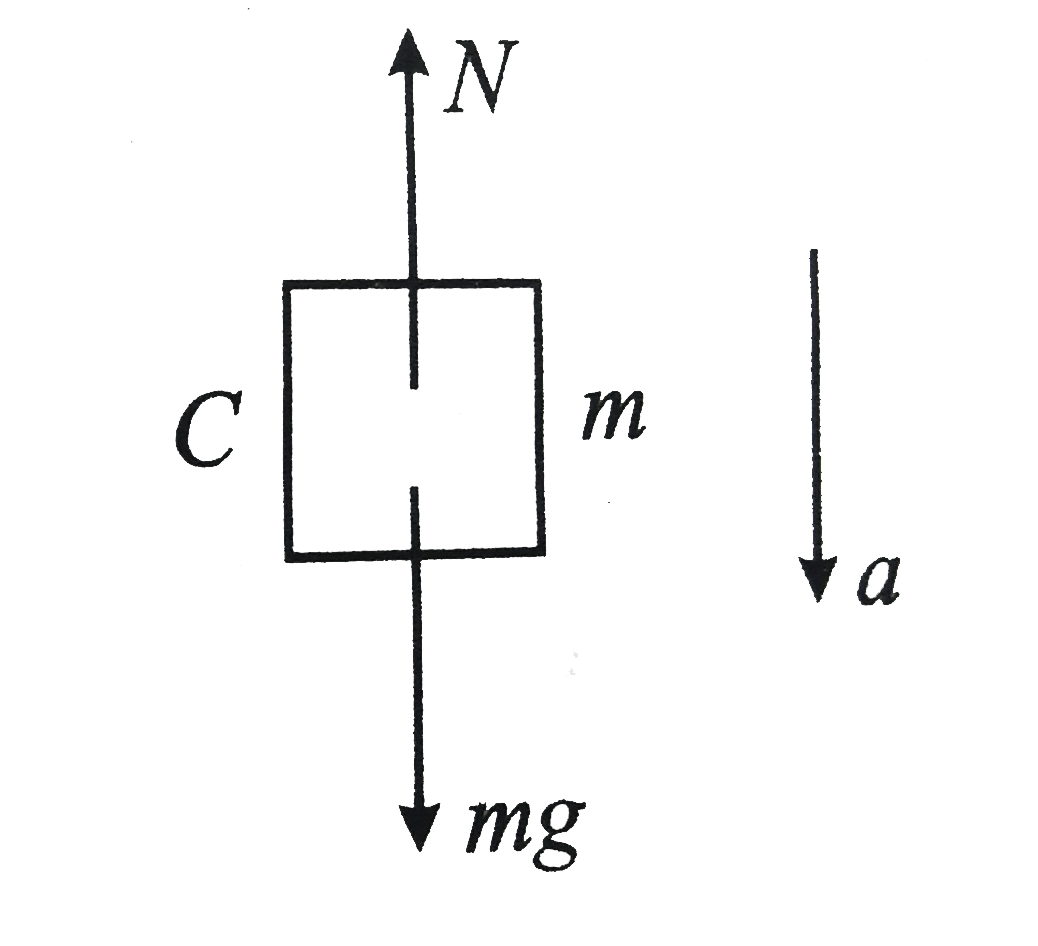
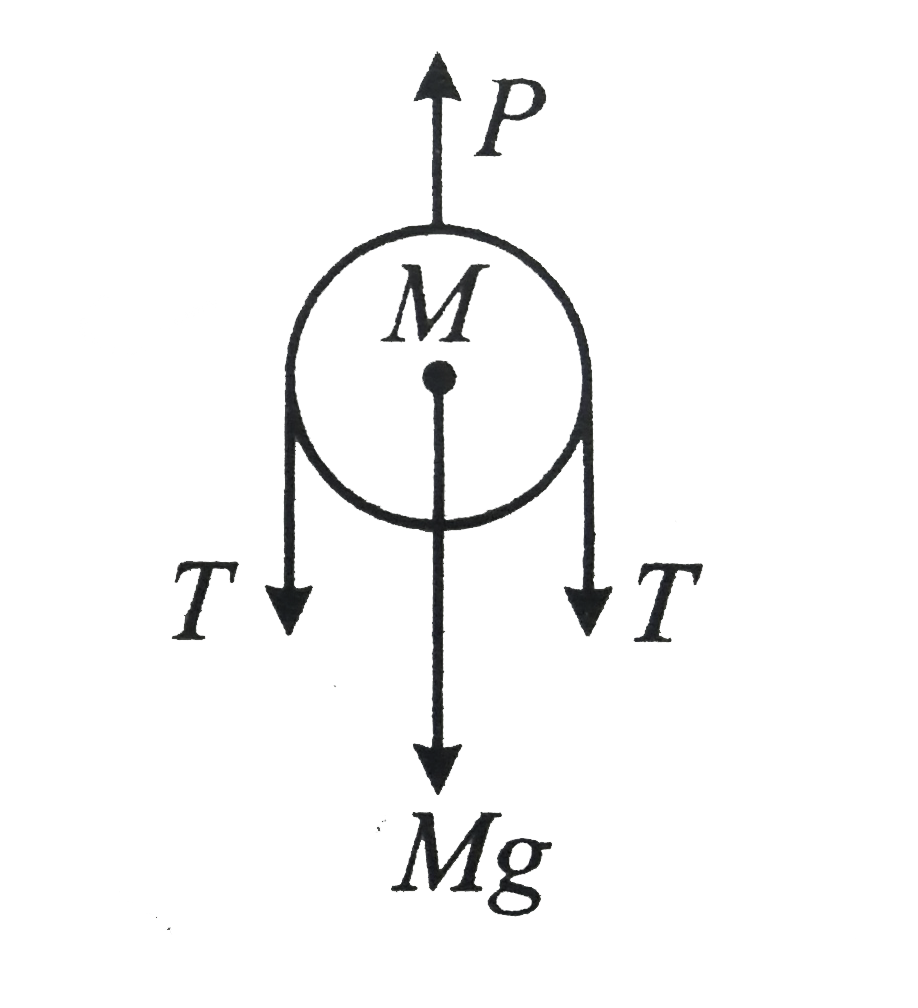
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- For the following system shown assume that pulley is frictionless, str...
Text Solution
|
- The system shown in fig, is released from rest. Calculate the tension ...
Text Solution
|
- For the following system shown assume that pulley is frictionless, str...
Text Solution
|
- For the following system shown assume that pulley is frictionless, str...
Text Solution
|
- For the following system shown assume that pulley is frictionless, str...
Text Solution
|
- Find the acceleration of the block of mass m. Assume pulleys are massl...
Text Solution
|
- In the shown mass pulley system, pulleys and string are massless. The ...
Text Solution
|
- In the system shown in fig the pulley is frictionless and the string m...
Text Solution
|
- Assume that all the pulleys are massless and frictionless and strings ...
Text Solution
|