Home
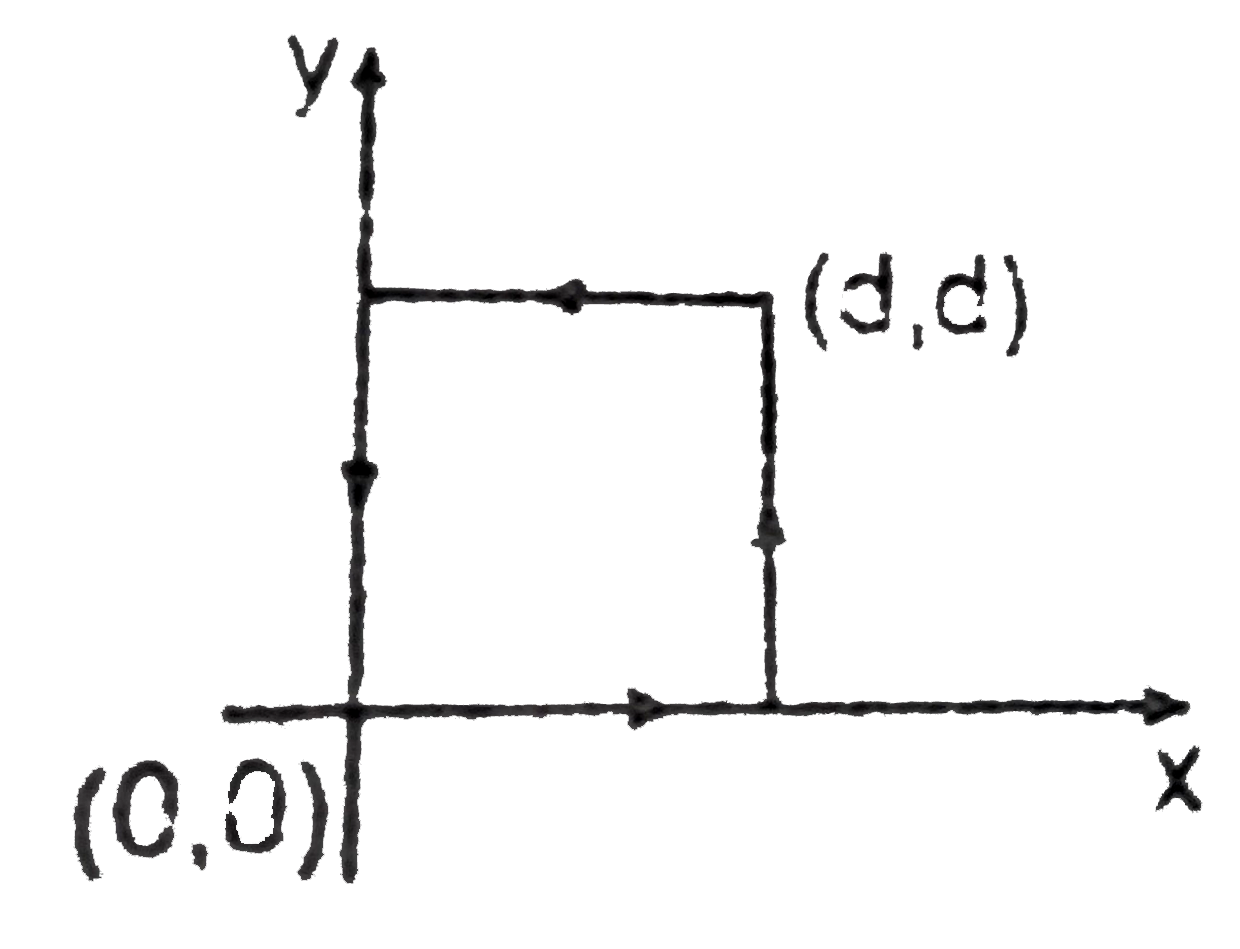
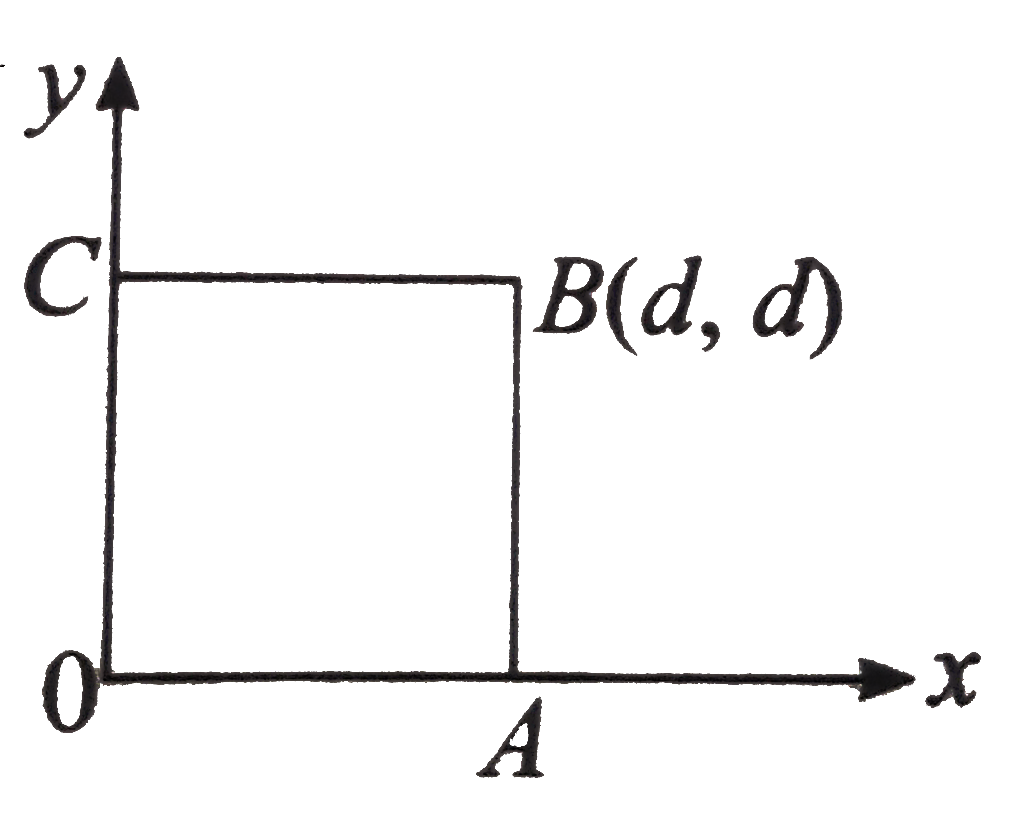
Class 12
PHYSICS
The work done by the force F=A(y^(2)hat(...

The work done by the force `F=A(y^(2)hat(i)+2x^(2)hat(j))`, where A is a constant and x & y are in meters around the path shown in

A

zero

B

`Ad`

C

`Ad^2`

D

`Ad^3`

Text Solution

Verified by Experts

The correct Answer is:
D

`intvecFdvecx=intA(y^2hati+2x^2hatj)(dxhati+dyhatj)`
`Aint(y^2dx+2x^2dy)`
`W_(OA)=0+0`,`W_(AB)=A[0+2d^2d]`
`W_(BC)=A[d^2(-d)+0]`,`W_(CD)=A[0+0]`
`W=0+2Ad^3-Ad^3+0=Ad^3`
Promotional Banner

Similar Questions

Explore conceptually related problems

The work done by the force vec(F)=A(y^(2) hati+2x^(2)hatj) , where A is a constant and x & y are in meters around the path shown is :

A particle is moving with velocity vecv = k( y hat(i) + x hat(j)) , where k is a constant . The genergal equation for its path is

A particle is moving with velocity vecv = k( y hat(i) + x hat(j)) , where k is a constant . The genergal equation for its path is

A particle is moving with velocity vecv = k( y hat(i) + x hat(j)) , where k is a constant . The genergal equation for its path is

A body of mass 1 kg begins to move under the action of a time dependent force F=(2that(i)+3t^(2)hat(j))N, "where" hat(i)and hat(j) are unit vector along x and y axis. What power will be developed by the force at the time?

If vec(E)=2x^(2) hat(i)-3y^(2) hat(j) , then V (x, y, z)

A body of mass 1 kg begins to move under the action of a time dependent force vec F = (2 t hat i + 3 t^(2) hat j) N , where hat i and hat j are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?

The work done by a force vec(F)=(-6x^(3)hat(i)) N in displacing a particle from x = 4m to x = - 2m is

A force vec(F)=(-y hat(i)+ x hat(j))N acts on a particle as it moves in an anticlockwise circular motion in x-y plane. The centre of the circle is at the origin. If the work done by the force is 32 pi J in one complete revolution then asSigmaing x, y to be in meters, find the radius of the path.

The work done by the force vec( F ) = 6 hat(i) + 2 hat(j) N in displacing an object from vec( r_(1)) = 3 hat(i) + 8 hat( j) to vec( r_(2)) = 5 hat( i) - 4 hat(j) m , is