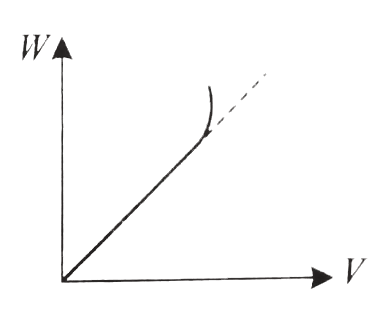
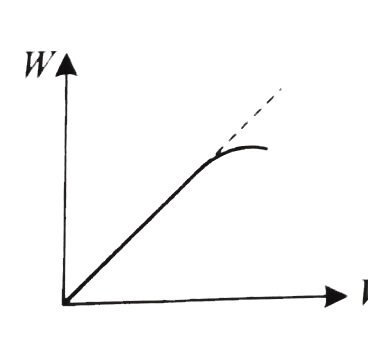
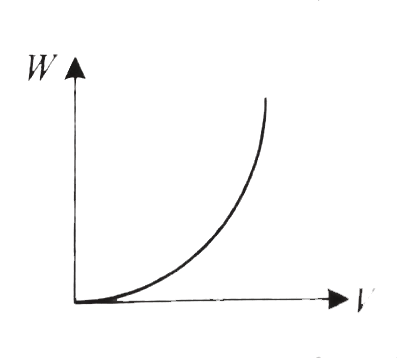
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle initially at rest on a frictionless horizontal surface, is ...
Text Solution
|
- A particle initially at rest on a frictionless horizontal surface, is ...
Text Solution
|
- A box of mass m=2 kg resting on a frictionless horizontal ground is ac...
Text Solution
|
- A particle initially at rest on a smooth horizontal surface, is acted ...
Text Solution
|
- A paticle is acted upon by a force of constant magnitude which always ...
Text Solution
|
- A particle at rest on a frictionless table is acted upon by a horizont...
Text Solution
|
- The displacement-time graph of a particle acted upon by a constant for...
Text Solution
|
- A particle of mass m initially moving with speed v.A force acts on the...
Text Solution
|
- To keep a particle moving with constant velocity on a frictionless hor...
Text Solution
|