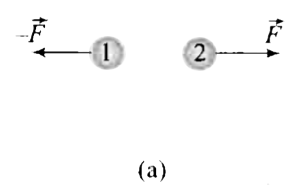
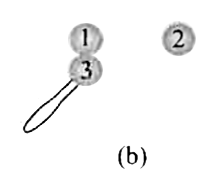
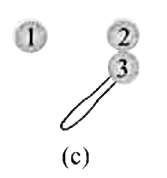
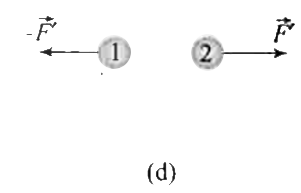
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
COULOMB LAW AND ELECTRIC FIELD
CENGAGE PHYSICS ENGLISH|Exercise Subjective|32 VideosCOULOMB LAW AND ELECTRIC FIELD
CENGAGE PHYSICS ENGLISH|Exercise Single Correct|47 VideosCOULOMB LAW AND ELECTRIC FIELD
CENGAGE PHYSICS ENGLISH|Exercise Exercises|58 VideosCENGAGE PHYSICS DPP
CENGAGE PHYSICS ENGLISH|Exercise subjective type|51 VideosELECTRIC CURRENT & CIRCUITS
CENGAGE PHYSICS ENGLISH|Exercise Kirchhoff s law and simple circuits|15 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-COULOMB LAW AND ELECTRIC FIELD-Subjective Type
- Calculate the number of electrons in a small, electrically neutral sil...
Text Solution
|
- A charged particle of radius 5xx10^(-7)m is located in a horizontal el...
Text Solution
|
- A glass rod rubbed with silk is brought close to two uncharged metalli...
Text Solution
|
- Indentical isolated conduction sphers 1 and 2 have equal charges and a...
Text Solution
|
- In Fig. a, particle 1 (of charge q(1)) and particle 2 (of charge q(2))...
Text Solution
|
- Figure (a) shows an arrangement of three charged particles separted by...
Text Solution
|
- Two positive point charges each of magnitude 10 C are fixed at positio...
Text Solution
|
- Four point positive charges are held at the vertices of a square in a ...
Text Solution
|
- A square loop of side 'l' having uniform linear charge density 'lambda...
Text Solution
|
- Figure shows the electric field lines around three point charges A,B a...
Text Solution
|
- Five charges, q each are placed at the coreners of a regular pentagone...
Text Solution
|
- In a certain region of space, electric field is along the z-direction ...
Text Solution
|
- Electric dipole of moment vec(P)=P hat(i) is kept at a point (x, y) in...
Text Solution
|
- A dipole with an electric moment vec(p) is located at a distance r fro...
Text Solution
|
- Light of wavelength 3000A is incident on a thin glass plate of refract...
Text Solution
|