Home
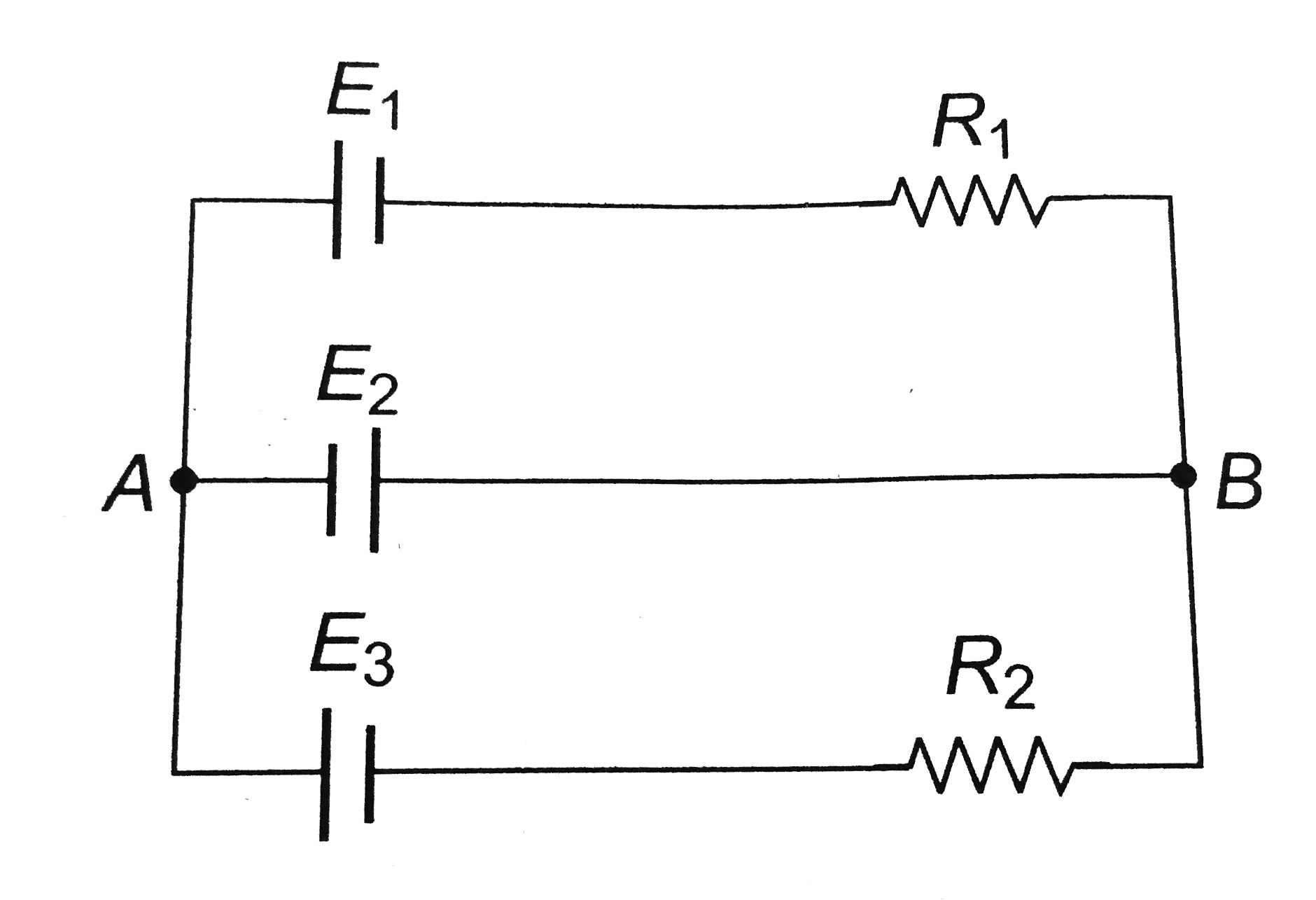
Class 12
PHYSICS
In the circuit shown here, E(1) = E(2) =...

In the circuit shown here, `E_(1) = E_(2) = E_(3) = 2 V` and `R_(1) = R_(2) = 4 ohms`. The current flowing between point `A` and `B` through battery `E_(2)` is

A

zero

B

2A from A to B

C

2A from B to A

D

None of the above

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • ELECTRIC CURRENT & CIRCUITS

    CENGAGE PHYSICS ENGLISH|Exercise Kirchhoff s law and simple circuits|15 Videos

  • ELECTRIC CURRENT & CIRCUITS

    CENGAGE PHYSICS ENGLISH|Exercise Combination of Resistance 2|14 Videos

  • COULOMB LAW AND ELECTRIC FIELD

    CENGAGE PHYSICS ENGLISH|Exercise Single Answer Correct Type|22 Videos

  • ELECTRIC CURRENT AND CIRCUIT

    CENGAGE PHYSICS ENGLISH|Exercise Interger|8 Videos

Similar Questions

Explore conceptually related problems

In the circuit shown in fig. 5.265, E_1 = E_2 = E_3 = 2V and R_1 = R_2 = 4Omega. The current flowing between points A and B through battery E_2 is

In the circuit shown in fig. E_(1)=3V, E_(2)= 2V, E_(3)= 1V, R=r_(1)=r_(2)=r_(3)= 1 ohm . Find the potential difference between the points A and B and the currents through each branch.

In the circuit shown below E_(1) = 4.0 V, R_(1) = 2 Omega, E_(2) = 6.0 V, R_(2) = 4 Omega and R_(3) = 2 Omega . The current I_(1) is

In the circuit shown, E_(1)= 7 V, E_(2) = 7 V, R_(1) = R_(2) = 1Omega and R_(3) = 3 Omega respectively. The current through the resistance R_(3)

In the circuit shown, E_(1)= 7 V, E_(2) = 7 V, R_(1) = R_(2) = 1Omega and R_(3) = 3 Omega respectively. The current through the resistance R_(3)

For the circuit shown, with R_(1)=1.0Omega,R_(2)=2.0Omega,E_(1)=2V and E_(2)=E_(3)=4V , the potential difference between the points 'a' and 'b' is approximately (in V ):

In the given network of ideal cells and resistors, R_(1) = 1.0 Omega, R_(2) = 2.0 Omega, E_(1) = 2V and E_(2) = E_(3) = 4V . The potential difference between the point a and b is

In the circuit in figure E_1=3V, E_2=2V, E_3=1V and R=r_1=r_2=r_3=1Omega Find the potential differece between the points A and B and the currents through each branch.

In the circuit shown below, E_(1)=17V,E_(2)=21V,R_(1)=2Omega,R_(2)=3Omega and R_(3)=5Omega . Using Kirchhoff.s laws, find the currents flowing through the resistors R_(1),R_(2) and R_(3) . (Internal resistance of each of the batteries is negligible.)

In the circuit shown in fig. E_(1)=3" volt",E_(2)=2" volt",E_(3)=1" vole and "R=r_(1)=r_(2)=r_(3)=1 ohm. (i) Find potential difference in Volt between the points A and B with A & B unconnected. (ii) If r_(2) is short circuited and the point A is coneted to point B through a zero resistance wire, find the current through R in ampere.