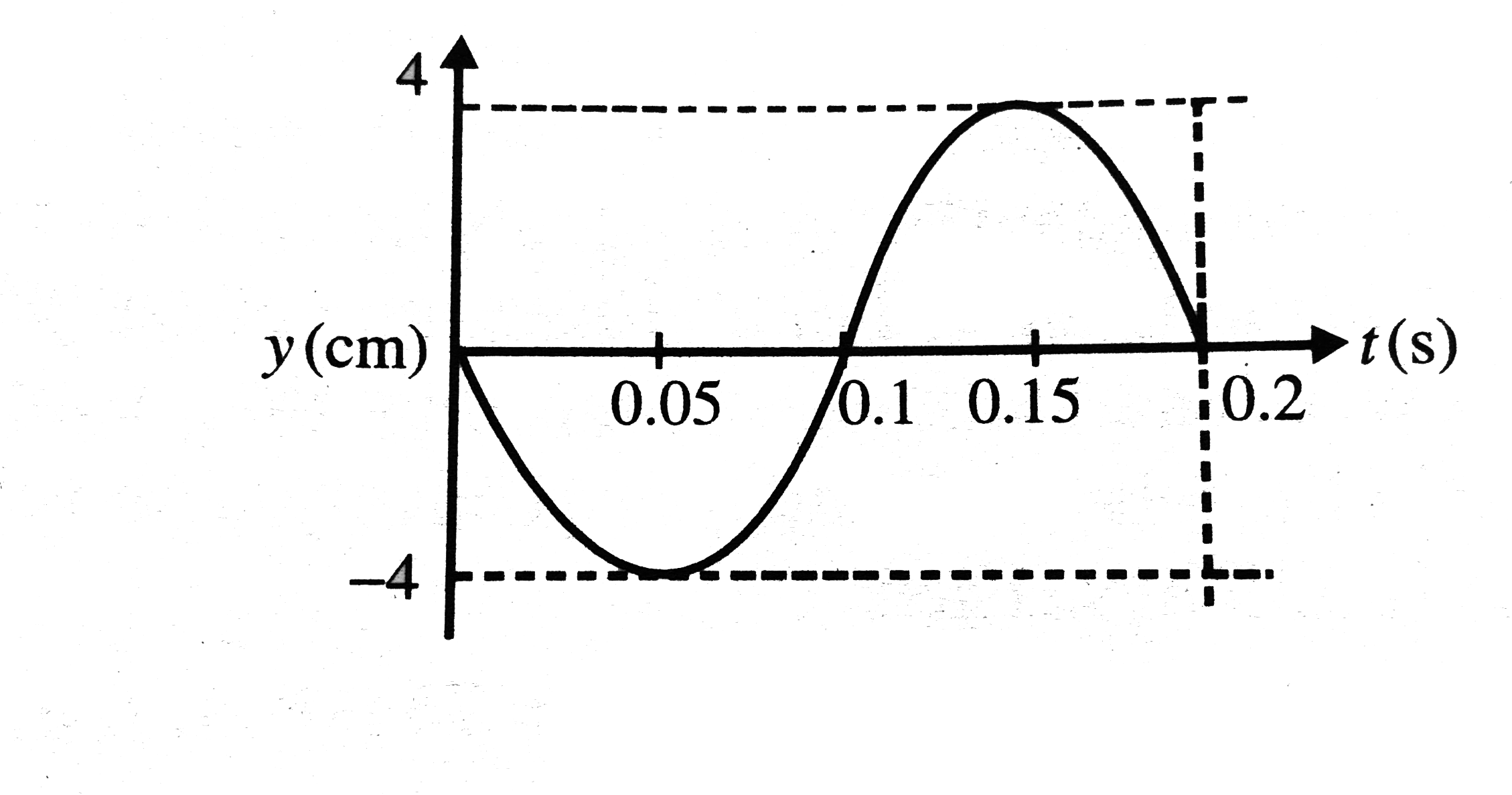Home
Class 11
PHYSICS
For a certain transverse standing wave o...

For a certain transverse standing wave on a long string , an antinode is formed at ` x = 0` and next to it , a node is formed at `x = 0.10 m` , the displacement `y(t)`of the string particle at `x = 0` is shown in Fig.7.97.

A

Transverse displacement of the particle at x = 0.05 m and t = 0.05 s is `-2 sqrt(2)cm`

B

Transverse displacement of the particle at x = 0.04 m and t = 0.025 s is `-2sqrt(2)cm`

C

Speed of the travelling waves that interfere to produce this standing wave is `2 m//s`

D

The transverse velocity of the string particle at ` x=(1)/(15)m` and t = 0.1 s is `20 cm//s`

Text Solution

Verified by Experts

The correct Answer is:
A, C, D
Promotional Banner

Topper's Solved these Questions

  • SUPERPOSITION AND STANDING WAVES

    CENGAGE PHYSICS ENGLISH|Exercise Fill in the Blanks Type|34 Videos

  • SUPERPOSITION AND STANDING WAVES

    CENGAGE PHYSICS ENGLISH|Exercise Subjective Type|2 Videos

  • SUPERPOSITION AND STANDING WAVES

    CENGAGE PHYSICS ENGLISH|Exercise Single Correct Answer Type|56 Videos

  • SOUND WAVES AND DOPPLER EFFECT

    CENGAGE PHYSICS ENGLISH|Exercise Integer|16 Videos

  • THERMODYNAMICS

    CENGAGE PHYSICS ENGLISH|Exercise 24|1 Videos

Similar Questions

Explore conceptually related problems

A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure. Q. The velocity of propagation of the wave is ?

A transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0.

A standing wave of time period T is set up in a string clamped between two rigid supports, At t =0 antinode is at its maximum displacement 2A .

A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure. The equation of the wave with all the constants evaluated is:

In a standing wave 4 nodes and 3 antinodes are formed between two fixed end of string of length 6 m.Then the wave length of the standing wave is

The wave funcation for a travelling wave on a string in given as y (x, t) = (0.350 m) sin (10 pi t - 3pix + (pi)/(4)) (a) What are the speed and direction of travel of the wave ? (b) What is the vertical displacement of the string at t = 0, x = 0.1 m ?

A wave of length 2m is superposed on its reflected wave to form a stationary wave. A node is located at x = 3m. The next node will be located at x=

Adjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0. (a) find the displacement of a point on the string as a function of position and time. (b) Find the speed of propagation of a transverse wave in the string. (c) Find the amplitude at a point 3.0 cm to the right of an antinode.

A transverse wave travelling on a taut string is represented by: Y=0.01 sin 2 pi(10t-x) Y and x are in meters and t in seconds. Then,

The wave-function for a certain standing wave on a string fixed at both ends is y(x,t) = 0.5 sin (0.025pix) cos500t where x and y are in centimeters and t is seconds. The shortest possible length of the string is :