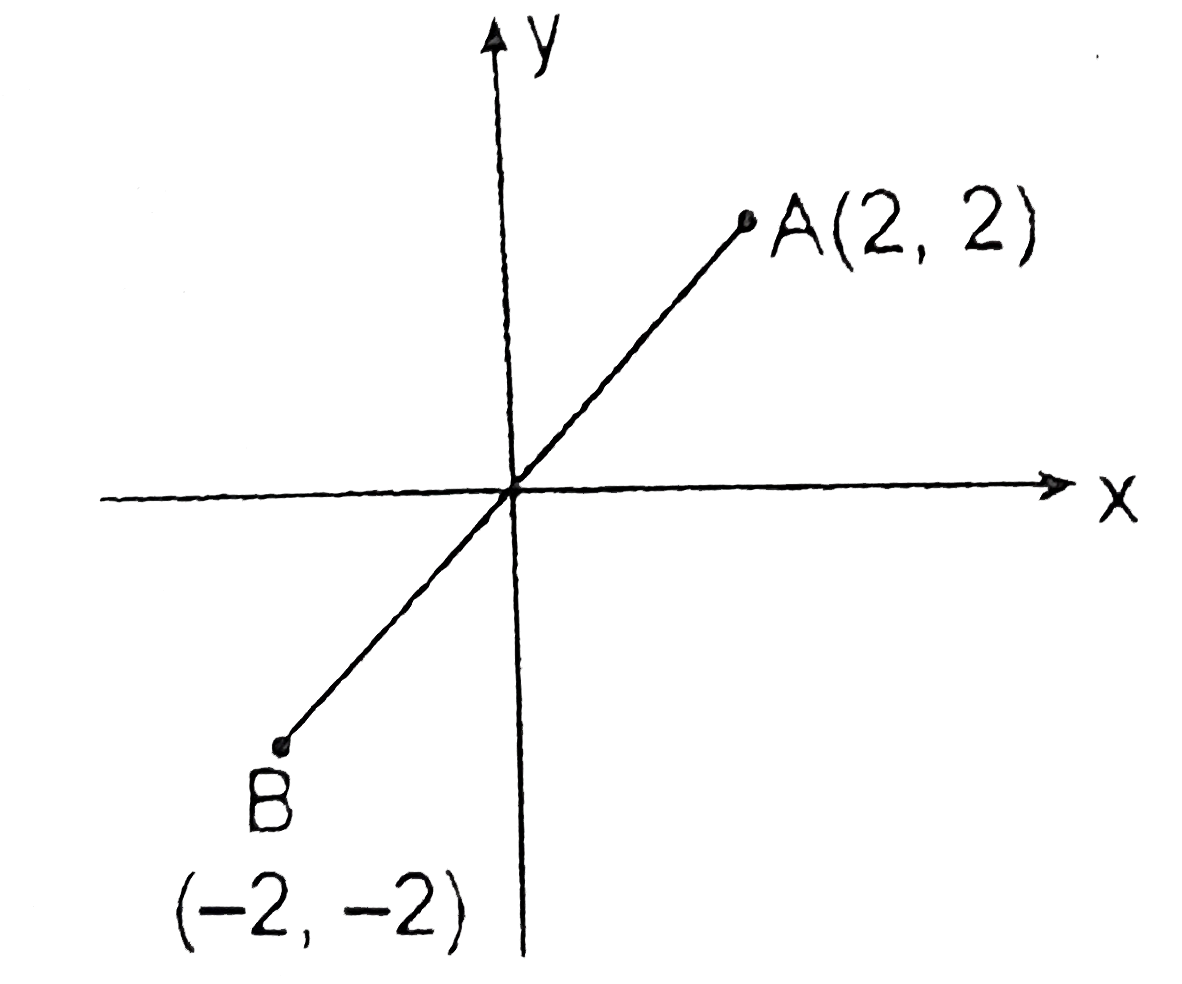
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass m = 2kg executes SHM in xy- plane between point A a...
Text Solution
|
- A particle of mass m free to move in the x - y plane is subjected to a...
Text Solution
|
- When forces F(1) , F(2) , F(3) are acting on a particle of mass m such...
Text Solution
|
- A particle of mass m = 2kg executes SHM in xy - plane between point A ...
Text Solution
|
- A particle of mass m is subjected to a force vecF=F(0)[cos (t)hati+sin...
Text Solution
|
- A particle starts from origin t = 0 with velocity 10.0 hatj ms^(-1) an...
Text Solution
|
- A force given by vecF=f(x)hati+f(y)hatj+f(z)hatk acts on a particle wh...
Text Solution
|
- बल F(1),F(2) और F(3) एक m द्रव्यमान के कण , पर इस प्रकार कार्य कर रह...
Text Solution
|
- समय t पर, त्वरण f से x-अक्ष पर गति करते कण का समीकरण f=f(0)(1-(1)/(T))...
Text Solution
|